Parametrizarea cu radical şi proprietăţile semi-cardioidei
De obicei, proprietăţile unei curbe precum cardioida $$f(x,y)=(x^2-ax+y^2)^2-a^2(x^2+y^2)=0\quad\small(a\ne 0)$$ se stabilesc - elegant - folosind "forma polară" a ecuaţiei (v. Cardioid). În mod tacit, atât ecuaţia implicită, cât şi ecuaţia polară angajează "la fel" toate punctele curbei (şi este greu de crezut că s-ar mai putea evidenţia proprietăţi nedisecate deja, ale acesteia). Dar este firească şi ideea de a "separa" cumva punctele curbei, concentrând atenţia pe o anumită ramură; apoi, ar fi de văzut şi familia de curbe (sau de ramuri) când $a$ variază.
Simetria faţă de axă şi parametrizări cu radical
Avem $f(x,y)=0 \Leftrightarrow f(x,-y)=0$, deci graficul este simetric faţă de $Ox$; semicardioida $\mathcal{S}$ este $f(x,y)=0$ cu $y\ge 0$; vom mai nota cu $\mathcal{F}$, familia semicardioidelor $\mathcal{S}$ (având acelaşi nod $O$, aceeaşi axă $Ox$ şi vârfurile în dreapta nodului).
O parametrizare tipică pentru un grafic simetric faţă de axa $Ox$ ar fi $x=u(t),\,y=\pm\sqrt{v(t)}$ cu $u$ şi $v$ funcţii raţionale (nu vrem circulare, ca în cazul unei "forme polare") de parametrul $t$; ar fi posibile mai multe asemenea parametrizări (echivalente) şi pe baza uneia găsite deja, am putea obţine o reparametrizare care să producă expresii (de exemplu, pentru derivată) mai convenabile.
(De sesizat că prin "ar fi posibile" am lăsat loc de excepţii; nu orice grafic este parametrizabil)
Se poate proba (şi justifica) faptul că graficele $f(x,y)$ pentru $\pm\,a$ sunt simetrice faţă de $Oy$, astfel că este suficient să considerăm $a\gt 0$. Plecăm de la o observaţie evidentă: orice punct $(x,y)$ din plan se află pe un anumit cerc centrat în origine; deci există $t\ge 0$ (şi este unic) încât $x^2+y^2=at^2$. Atunci, $f(x,y)=0$ s-ar rescrie sub forma $(t^2-x)^2-at^2=0$, adică $(t^2-x-\sqrt{a}t)(t^2-x+\sqrt{a}t)=0$ (unde $a\gt 0$).
Dar posibilitatea $t^2-x+\sqrt{a}t=0$ trebuie exclusă, fiindcă ar conduce la $y^2\le 0$ (am găsi $y^2=at^2-x^2=at^2-(t^2+\sqrt{a}t)^2=-t^3(t+2\sqrt{a})$ şi cu $t\gt 0$ am avea $y^2\lt 0$ - absurd).
Deci neapărat, $t^2-x-\sqrt{a}t=0$ - de unde $x=t(t-\sqrt{a})$; iar în acest caz, avem $y^2\small=at^2-x^2=at^2-t^2(t-\sqrt{a})^2\normalsize=t^2\cdot t(2\sqrt{a}-t)$ şi $y^2\ge 0 \Leftrightarrow t\in[0,2\sqrt{a}]$.
Conchidem că parametrizarea încercată are sens: cercurile $x^2+y^2=at^2$ taie graficul $f(x,y)=0$ în cel mult două puncte care sunt simetrice faţă de $Ox$, ceea ce înseamnă că punctele semi-cardioidei superioare $\mathcal{S}$ pot fi exprimate în mod unic prin parametrul $t$: $$x=t(t-\sqrt{a}), \quad y=t\sqrt{t(2\sqrt{a}-t)};\quad t\in[0,2\sqrt{a}]$$
Aceasta este absolut suficientă pentru a investiga proprietăţile lui $\mathcal{S}$ (şi a restabili eventual, proprietăţi cunoscute ale cardioidei); dar când am viza proprietăţi ale familiei $\mathcal{F}$ (pentru care şi $a$ este un parametru variabil), această parametrizare (în care $t$ depinde de $a$) ar fi neconvenabilă.
Putem elimina dependenţa între $t$ şi $a$, scalând faţă de lungimea intervalului iniţial: $t=2\sqrt{a\,}\lambda$, cu $\lambda\in[0,1]$; noua parametrizare a lui $\mathcal{S}$ - renotând totuşi '$\lambda$' cu '$\,t\,$' - este:
Această exprimare este categoric mai avantajoasă faţă de cea anterioară; de exemplu, acum vedem imediat că $\frac{y}{x}$ nu depinde de $a$, aceasta însemnând că punctele corespunzătoare unei aceleiaşi valori $t\in[0,1]$ pe semicardioidele din $\mathcal{F}$ sunt situate pe o aceeaşi dreaptă care trece prin nodul comun $O$ (bineînţeles că, simetrizând faţă de $Ox$, putem reformula proprietatea şi pentru cardioidele deduse din $\mathcal{F}$).
Proprietăţi ale semi-cardioidei
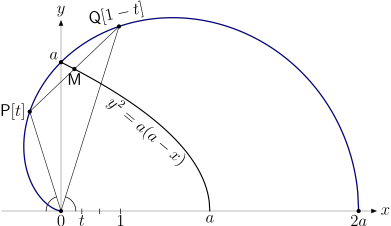
Când este cazul, vom specifica în paranteză pătrată valoarea (sau expresia) parametrului din care provin coordonatele punctului; considerăm punctele $\mathsf{P}\equiv\mathsf{P}[t]$ şi $\mathsf{Q}\equiv\mathsf{Q}[1-t]$, provenite din valori simetrice faţă de mijlocul $\frac{1}{2}$ al intervalului $[0,1]$ pe care variază $t$. Următoarea figură (pentru $a\gt 1$) sintetizează unele proprietăţi pe care le vom stabili mai jos:
Avem întâi câteva constatări imediate:
(1) $\mathsf{OP}=2at\quad (t\in[0,1])$
(2) $\mathsf{OP}+\mathsf{OQ}=2a$
(3) Triunghiurile $\mathsf{OPP'}$ şi $\mathsf{OQQ'}$ sunt (invers) asemenea - unde $\mathsf{P'}$ şi $\mathsf{Q'}$ sunt proiecţiile pe $Ox$ ale punctelor $\mathsf{P}$ şi $\mathsf{Q}$.
Într-adevăr, din substituţiile iniţiale $x^2+y^2=at^2$ şi $t\equiv 2\sqrt{a\,}t$ rezultă (1). Aplicând (1) pentru $\mathsf{Q}$ avem: $\small\mathsf{OQ}=\mathsf{OQ}[1-t]=2a(1-t)=2a-\mathsf{OP}$, adică (2).
Observăm (în treacăt) că $\mathsf{P}$ şi $\mathsf{Q}$ sunt focarele unei elipse care trece prin $O$ şi are semiaxa mare $a$ (şi ar fi de clarificat această conjectură, cam artificială: locul focarelor elipselor care trec origine şi au aceeaşi axă mare este format din două cardioide simetrice faţă de $Oy\,$?!).
Coordonatele lui $\mathsf{P}[t]$ sunt $x_{\small\mathsf{P}}\small=2at(2t-1)$ şi $y_{\small\mathsf{P}}\small=4at\sqrt{t(1-t)}$ iar cele ale lui $\mathsf{Q}[1-t]$ sunt $x_{\small\mathsf{Q}}\small=2a(1-t)(1-2t)$ şi $y_{\small\mathsf{Q}}\small=4a(1-t)\sqrt{t(1-t)}$; rezultă $\frac{y_{\small\mathsf{P}}}{y_{\small\mathsf{Q}}}=-\frac{x_{\small\mathsf{P}}}{x_{\small\mathsf{Q}}}=\frac{\mathsf{OP}}{\mathsf{OQ}}=\frac{t}{1-t}$ încât avem şi (3) - exceptând pentru $t$ valorile $0,1$ şi $\frac{1}{2}$ corespunzătoare "nodului" $O(0,0)$ şi "vârfului" $\mathsf{A}(2a,0)$, respectiv punctului $\mathsf{B}(0,a)$ în care $\mathcal{S}$ taie $Oy$.
Raportul absciselor punctelor $\mathsf{P}$ şi $\mathsf{Q}$ fiind negativ, urmează că unul dintre ele este situat pe arcul semicardioidei din stânga axei $Oy$, iar celălalt este pe arcul din dreapta.
Din (3) rezultă că $\mathsf{OP}$ şi $\mathsf{OQ}$ sunt egal înclinate faţă de $Ox$ (adică faţă de baza $\mathsf{OA}$); altfel spus, $Oy$ bisectează unghiul $\mathsf{POQ}$ (sau încă, unghiurile polare ale lui $\mathsf{P}$ şi $\mathsf{Q}$ sunt suplementare).
Mai rezultă că, dacă $\mathsf{Q}_1$ este simetricul lui $\mathsf{Q}$ faţă de $Ox$ (aflat pe semi-cardioida inferioară), atunci triunghiurile $\mathsf{OPP'}$ şi $\mathsf{OQ}_1\mathsf{Q'}$ sunt direct asemenea - de unde rezultă că $\mathsf{P}$, $\mathsf{O}$ şi $\mathsf{Q}_1$ sunt coliniare şi $\mathsf{PQ}_1=2a$; am regăsit astfel, proprietatea binecunoscută: coardele cardioidei duse prin nodul $\mathsf{O}$ au aceeaşi lungime.
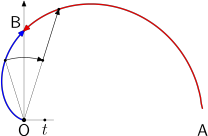 Axa $Oy$ desparte semicardioida în două arce astfel încât punctele unuia provin din punctele celuilalt prin câte o anumită rotaţie şi scalare: când $t$ parcurge $[0,\frac{1}{2}]$, punctul $\mathsf{P}[t]$ parcurge în sens orar arcul $\mathsf{(OB)}$ (din stânga axei $Oy$); rotind fiecare punct $\mathsf{P}$ cu unghiul $\theta(t)$ şi scalând rezultatul cu factorul $k(t)$ se obţin (în sens antiorar) respectiv punctele arcului $\mathsf{(AB)}$ - unde (cum rezultă din (3)) $\theta(t)\small=2\measuredangle(\mathsf{POB})$, iar $k(t)=\frac{1-t}{t}\mathsf{OP}$ (dar cu $t\ne 0$).
Axa $Oy$ desparte semicardioida în două arce astfel încât punctele unuia provin din punctele celuilalt prin câte o anumită rotaţie şi scalare: când $t$ parcurge $[0,\frac{1}{2}]$, punctul $\mathsf{P}[t]$ parcurge în sens orar arcul $\mathsf{(OB)}$ (din stânga axei $Oy$); rotind fiecare punct $\mathsf{P}$ cu unghiul $\theta(t)$ şi scalând rezultatul cu factorul $k(t)$ se obţin (în sens antiorar) respectiv punctele arcului $\mathsf{(AB)}$ - unde (cum rezultă din (3)) $\theta(t)\small=2\measuredangle(\mathsf{POB})$, iar $k(t)=\frac{1-t}{t}\mathsf{OP}$ (dar cu $t\ne 0$).
Un calcul diferenţial elementar ne arată proprietăţile punctelor $\mathsf{O}$, $\mathsf{B}$ şi $\mathsf{A}$ şi evidenţiază alte puncte importante ale semicardioidei (şi proprietăţi ale familiei $\mathcal{F}$). Avem
$$\frac{\mathsf{d}y}{\mathsf{d}x}=\frac{\mathsf{d}y/\mathsf{d}t}{\mathsf{d}x/\mathsf{d}t}=\frac{\sqrt{t\,}(3-4t)}{(4t-1)\sqrt{1-t}}\quad\quad(t\small\in[0,1]-\{1/4,1\})$$.Obs. Pentru obţinerea derivatei (sau pentru verificarea calculului propriu) se poate folosi eventual, un "widget" de calcul simbolic (v. Wolfram Mathematica):
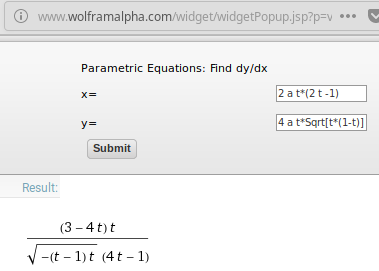
(simplificând cu $\small\sqrt{t}$, rezultatul afişat revine la cel redat mai sus, obţinut desigur prin calcul direct)
Avem $\left.\frac{\mathsf{d}y}{\mathsf{d}x}\right|_{t=\frac{1}{2}}\small=1$, deci tangenta în $\mathsf{B}[t=\frac{1}{2}]$ este paralelă cu prima bisectoare (din $\small xOy$).
$\left.\frac{\mathsf{d}y}{\mathsf{d}x}\right|_{t\rightarrow 0}\small=0$, deci cardioida este tangentă în nodul $\mathsf{O}$, axei $Ox$; $\left.\frac{\mathsf{d}y}{\mathsf{d}x}\right|_{t\rightarrow 1}\small=\infty$ deci tangenta în vârful $\mathsf{A}$ este verticală.
Să observăm că avem tangentă orizontală şi în punctul dat de $t_1=\frac{3}{4}$ şi avem tangentă verticală şi în punctul dat de $t_2=\frac{1}{4}$ (pentru care derivata se anulează, respectiv devine $\infty$). Rezultă că punctul cel mai de sus ("Upper") al semicardioidei este $\mathsf{P}[t=t_1]=\mathsf{U}(\frac{3a}{4},\,\frac{3\sqrt{3\,}a}{4})$, iar punctul cel mai din stânga ("Left") este $\mathsf{P}[t=t_2]=\mathsf{L}(-\frac{a}{4},\,\frac{\sqrt{3\,}a}{4})$.
Observând că $\small t_1+t_2=1$, deducem că $\mathsf{L}$ şi $\mathsf{U}$ sunt precum $\mathsf{P}$ şi $\mathsf{Q}$ din relaţia (2); deci (având în vedere ce am dedus mai sus din (3)) dreptele $\mathsf{OL}$ şi $\mathsf{OU}$ sunt simetrice faţă de $Oy$. Panta dreptei $\mathsf{OU}$ este $\sqrt{3}$, deci $\mathsf{OU}$ este înclinată cu $\small 60^{\circ}$ faţă de $Ox$; rezultă că $\measuredangle(LOU)=60^{\circ}$. Panta dreptei $\mathsf{LU}$ este $\frac{\sqrt{3}}{2}$, deci dreapta $\mathsf{LU}$ este înclinată cu $\small\mathsf{arctg\,}{\frac{\sqrt{3}}{2}}\approx 40.8934^{\circ}$ faţă de $Ox$.
Ar fi de subliniat că aceste ultime proprietăţi nu depind de $a$: toate subcardioidele din $\mathcal{F}$ au la fel înclinată (cu $\mathsf{arctg\,}{\frac{\sqrt{3}}{2}}$) dreapta care uneşte punctul cel mai din stânga şi punctul cel mai de sus, iar unghiul razelor polare ale acestor puncte este de $\small 60^{\circ}$; toate punctele $\mathsf{U}$ şi respectiv, toate punctele $\mathsf{L}$ sunt aşezate pe câte o dreaptă care trece prin nodul comun şi este înclinată cu $60^{\circ}$ şi respectiv $120^{\circ}$, faţă de axa comună. De fapt, fiindcă $\frac{\mathsf{d}y}{\mathsf{d}x}$ nu depinde de $a$, urmează că pentru orice $t\in[0,1]$ fixat, tangentele în punctele $\mathsf{P}[t]$ corespunzătoare pe subcardioidele din $\mathcal{F}$ sunt paralele; combinând cu o observaţie anterioară (punctele $\mathsf{P}[t]$ sunt pe o aceeaşi dreaptă care trece prin nod), rezultă: tangentele subcardioidelor din $\mathcal{F}$ în punctele de intersecţie cu o aceeaşi dreaptă dusă prin nodul comun, au aceeaşi direcţie.

Mai decurge ("simetrizând" faţă de $Ox$) că locul punctelor cel mai de sus, cel mai de jos şi cel mai din stânga pentru cardioidele cu acelaşi nod, aceeaşi axă şi cu vârfurile situate în dreapta nodului este format din două drepte care trec prin nod la $60^{\circ}$ şi respectiv $120^{\circ}$ faţă de axa comună.
Desigur, tangenta în $\mathsf{L}$ este perpendiculară pe $Ox$, iar tangenta în $\mathsf{U}$ este paralelă cu $Ox$; dar mai general: exprimând $\frac{\mathsf{d}y}{\mathsf{d}x}$ pentru punctele "conjugate" $\mathsf{P}(t)$ şi $\mathsf{Q}(1-t)$, constatăm că pantele tangentelor la semicardioidă în aceste puncte sunt inverse una celeilalte (pentru orice $t$ şi iarăşi, independent de $a$); deci (pentru fiecare $t$) unghiurile ascuţite formate de aceste două tangente cu axa $Ox$ sunt complementare (fiindcă $\mathrm{tg}\,\alpha\cdot\mathrm{tg}\,\beta=1\Rightarrow\cos(\alpha+\beta)=0\Rightarrow\alpha+\beta=\pm\frac{\pi}{2}+2\pi$).
Mijlocul $\mathsf{M}$ al segmentului $\mathsf{PQ}$ are coordonatele $x=a(2t-1)^2=a-4at(1-t)$ şi $y=2a\sqrt{t(1-t)}$ (şi este suficient să considerăm punctele $\mathsf{P}$ aflate pe arcul de semi-cardioidă din stânga axei $Oy$, cum am justificat mai sus); rezultă că atunci când $t$ parcurge $[0,\frac{1}{2}]$, punctul $\mathsf{M}$ parcurge arcul parabolei $y^2=a(a-x)$, cuprins între vârful acesteia $(a, 0)$ şi punctul $\mathsf{B}(0,a)$ (altfel spus, parabola cu focarul în $\mathsf{O}$ şi cu directoarea dată de tangenta cardioidei în $\mathsf{A}$ "mediază" între arcele despărţite de $Oy$ pe semi-cardioidă; v. prima dintre figurile de mai sus).
În schimb, mijlocul $\mathsf{M}_1$ al segmentului care uneşte $\mathsf{P}$ cu simetricul lui $\mathsf{Q}$ faţă de $Ox$ parcurge cercul de centru $(\frac{a}{2}, 0)$ şi rază $\frac{a}{2}$ (regăsim o proprietate cunoscută a mijloacelor coardelor duse prin nodul cardioidei). Într-adevăr, avem $x_{\mathsf{M}_1}=x_{\mathsf{M}}\small=a(2t-1)^2$ şi $y_{\mathsf{M}_1}\small=(y_{\mathsf{P}}+(-y_{\mathsf{Q}}))/2$, adică $y_{\mathsf{M}_1}\small=2a\sqrt{t(1-t)}(2t-1)$; observând că $a-x_{\mathsf{M}_1}=4at(1-t)$ rezultă $y_{\mathsf{M}_1}^2=(a-x_{\mathsf{M}_1})x_{\mathsf{M}_1}$, deci $\mathsf{M}_1$ se află pe cercul $x^2+y^2-ax=0$.
Desigur, putem regăsi astfel (prin exprimarea parametrică stabilită mai sus pentru punctele $\mathsf{P}$ ale semicardioidei) diverse alte proprietăţi ale cardioidei (şi le putem eventual "îngusta", pentru semi-cardioidă). De exemplu, să verificăm că semi-cardioida este podara semicercului de centru $(a, 0)$ şi rază $a$ (adică este locul picioarelor perpendicularelor din $O$ pe tangentele semicercului):
panta perpendicularei $\delta$ duse în $\mathsf{P}$ pe $\mathsf{OP}$ este $-\frac{x_{\mathsf{P}}}{y_{\mathsf{P}}}=\frac{1-2t}{2\sqrt{t(1-t)}}$; ecuaţia dreptei $\delta$ (după eliminarea numitorului şi reduceri) este: $(1-2t)x-2\sqrt{t(1-t)}y+2at=0$; distanţa de la punctul $(a,0)$ la dreapta $\delta$ este $\frac{(1-2t)a+2ta}{\sqrt{(1-2t)^2+4t(1-t)}}=a$; prin urmare, $\delta$ este tangentă cercului de centru $(a,0)$ şi rază $a$ (şi de fapt, semicercului superior, al acestuia).
NB. De ce am indicat [1] şi [2], câtă vreme nu am făcut nicio referire la acestea?
Pe de o parte, am realizat figurile redate mai sus (şi am experimentat) folosind programe în MetaPost similare celor explicate deja în [2].
Pe de altă parte, în [1] ajunsesem la o ecuaţie complicată ("ireductibilă"), care se pare că nu intră în vreun catalog obişnuit: $\small(x^2+y^2)^4-3(x^2+y^2)^2-2(x^2-y^2)=0$; graficul (trasat "dintr-odată" - drept "curba de nivel 0" a suprafeţei $\small f(x,y)=z$) aminteşte de un "Dürer folium" - dar zicem că este format de fapt, din două pseudo-cardioide opuse faţă de $Oy$; am încercat să izolez această pseudo-cardioidă (plecând de la $x^2+y^2=2t$) iar dificultăţile apărute (prevestind un eşec) m-au făcut să încerc lămurirea lucrurilor pe o curbă "mai modestă", precum cardioida (aşa rezultând, cele prezentate mai sus).
vezi Cărţile mele (de programare)