Cum trasăm curba asociată unei funcţii?

Dacă funcţia este dată în mod explicit y = f(x) atunci: generăm o secvenţă deasă de abscise x, determinăm valorile funcţiei pe aceste abscise şi plotăm succesiv punctele rezultate. Dacă funcţia este dată implicit f(x,y) = 0 atunci: generăm o reţea cât mai fină de puncte (x,y), determinăm şi tabelăm valorile funcţiei în punctele reţelei şi plotăm punctele pentru care în tabel găsim 0.

Dar dacă limbajul respectiv prevede un anumit mecanism de interpolare, atunci pentru construcţia graficului ar putea fi suficientă indicarea doar a câtorva puncte (şi direcţionări).
MetaFont integrează interpolarea bazată pe cubice Bézier şi în [1] am construit astfel, lemniscata lui Bernoulli - plecând de la doar trei puncte (centrul, un vârf şi unul dintre punc­tele cel mai "înalte", împreună cu direcţiile a două tangente). Vrem să verificăm că putem proceda la fel şi pentru alte categorii de curbe; alegem trisectoarea lui Pascal:

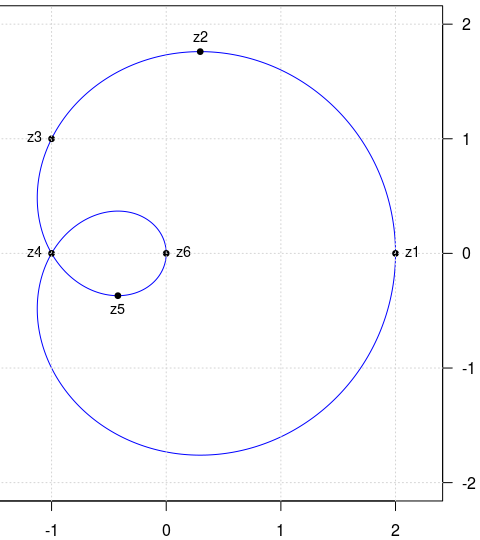
Am obţinut acest grafic prin programul R următor:

plot_path <- function(func2, ...) {  # plotează funcţii implicite
    x <- y <- seq(-2, 2, by=0.001)  # o reţea deasă, de 4000×4000 puncte (x,y)
    Z <- outer(x, y, func2)  # valorile f(x,y), indexate după x şi y
    contour(x, y, Z, levels = 0, drawlabels=FALSE, ...)  # graficul f(x,y) = 0
}  ## '...' transmite argumente specifice funcţiei apelate în interior, 'contour'

plot_path(function(u, v) (u^2+v^2)^2-3*(u^2+v^2)-2*u,  # din f(z) = z(z+1), |z|=1
          col="blue", asp=1)  # culoare, 'aspect-ratio' (de pasat lui 'contour()')

zpath <- c(2 + 0i,  # z1: punctul de plecare al arcului, cu tangentă verticală
    (-1+sqrt(33))/16 + 1i*sqrt((207+33*sqrt(33))/2)/8,  # z2: punctul cel mai înalt
    -1 + 1i, -1 + 0i,  # z3 (unde tangenta are panta egală cu 2) şi z4
    (-1-sqrt(33))/16 - 1i*sqrt((207-33*sqrt(33))/2)/8,  # minim pe bucla interioară
    -0 + 0i)  # z6 (originea) încheie arcul descris de 'zpath'
points(zpath, cex=0.8, pch=19)  # marchează punctele de referinţă din 'zpath'
text(zpath, paste0("z", 1:6), pos=c(4,3,2,2,1,4), cex=0.9)
grid(); axis(side=4, las=1)

plot_path() plotează funcţia implicită primită ca parametru, fie ea f(x,y): se constituie o reţea de puncte (x,y) (suficient de fină), se calculează şi se tabelează valorile funcţiei în punctele reţelei (folosind outer()) şi apoi se plotează (prin contour()) punctele reţelei în care valorile sunt nule (se obţine curba "de nivel 0" a suprafeţei Z=f(x,y), deci graficul ecuaţiei f(x,y) = 0).

Expresia funcţiei pentru care am invocat plot_path() (obţinând graficul redat mai sus) provine (cum vom arăta mai jos) din f(z) = z(z+1) unde z descrie cercul unitate.

Pe grafic am marcat punctele z1, z2, ..., z6 pe care intenţionăm să le constituim într-o structură MF de tip path, sperând că 'draw zpath' va completa suficient de exact arcul curbei care uneşte cele şase puncte indicate în zpath; vom arăta mai jos cum am calculat punctele z2 şi z4 (reprezentând valori extreme ale funcţiei) şi cum am determinat panta tangentei în z3.

Ecuaţia curbei şi determinarea tangentelor

Am arătat în [2], că funcţia complexă $f(z)=z(z+1)$ transformă cercul unitate $|\,z\,|=1$ în trisectoarea Pascal redată în imaginea de mai sus. Dar am procedat indirect, verificând geometric îndeplinirea proprietăţilor caracteristice necesare; acum –având de calculat panta pentru unele tangente– preferăm să ne bazăm pe ecuaţiile carteziene corespunzătoare.

Fie $z=x+iy$ (cu $x,y\in\mathbb{R}$ şi $i^2=-1$), astfel încât $x^2+y^2=1$; obţinem partea reală şi respectiv, imaginară a lui $z(z+1)$: $\eqalignno{u&=x^2-y^2+x&(1)\\v&=y(2x+1)&(2)\\&\small\mathrm{unde}\;x^2+y^2=1}$

Eliminând $x$ şi $y$, vom găsi ecuaţia curbei descrise de punctul $(u,v)$ (în planul $\small uOv$); ţinând cont că $\small y^2=1-x^2$, avem $\small u+1=x(2x+1)$ şi $\small (u+1)^2+v^2=(2x+1)^2$; rămâne de eliminat $x$ între relaţiile $\small u=2x^2+x-1$ şi $\small u^2+v^2=(2x+1)^2-2u=2(x+1)$. Rezultă ecuaţia:

$\eqalignno{(u^2+v^2)^2-3(u^2+v^2)-2u&=0&(3)}$

De aici avem funcţia indicată lui plot_path() în programul de mai sus. (3) exprimă în mod implicit ordonatele $v$ în funcţie de abscisele $u$ ale punctelor $(u,v)$ ale curbei; $\,v\,'$ (derivata lui $v$) ne va permite să calculăm pantele tangentelor care ne interesează.

Să derivăm (3) în raport cu $u$: $\;\small 2(u^2+v^2)(2u+2vv\,')-3(2u+2vv\,')-2=0$; separăm $\small u+vv\,'$ şi apoi găsim uşor: $\eqalignno{v\,'&=\frac{1-u(2(u^2+v^2)-3)}{v(2(u^2+v^2)-3)}&(4)}$

Punctul $(-1,1)$ - etichetat cu z3 pe figura de mai sus - satisface ecuaţia curbei (3); tangenta în acest punct are panta $v\,'(-1)=2$.

Punctele "cel mai înalte" ale curbei (de maxim sau minim local) le găsim rezolvând $v\,'=0$ împreună cu (3); din $v\,'=0$ avem $\small u^2+v^2=\normalsize \frac{1+3u}{2u}$ astfel că (3) conduce la ecuaţia

Aici, rădăcina evidentă $\small u=-1$ trebuie exclusă: din (3) ar rezulta în acest caz $\small v^2=0$ (ceea ce ar anula numitorul în (4)), sau $\small v^2=1$ (care ar contrazice $\small v\,'=0$). Celelalte două rădăcini ale ecuaţiei (5) sunt $\small u_{1,2}=(-1\pm\sqrt{33\,})/16$ şi calculând cu atenţie, din $\small v^2=(1+3u)/2u-u^2$ găsim şi "înălţimile" corespunzătoare $\small v_{1,2}=\pm\sqrt{(207\pm33\sqrt{33})/2\,}/8$ (de unde avem coordonatele punctelor z2 şi z5 în variabila zpath, din programul de mai sus).

S-a dovedit că n-ar fi nevoie să precizăm în programul MF următor şi direcţia tangentei în z4 (punctul (-1,0) exclus mai sus pentru ecuaţia (5)). Totuşi, ce pante au cele două tangente în punctul dublu z4? Am arătat în [2] că dacă P este un punct pe bucla mare a curbei, iar Q este intersecţia cu bucla interioară a dreptei PA (unde A ≡ z4), atunci mijlocul segmentului PQ se află pe cercul unitate (centrat în O ≡ (0,0), de rază OA=1); punctul P ≡ $\small(0, \sqrt{3})$ aparţine curbei (fiindcă verifică ecuaţia (3)), iar mijlocul segmentului AP este $\small(-1/2, \sqrt{3}/2)$ şi evident, aparţine cercului unitate - cu alte cuvinte, în acest caz Q ≡ A adică PA este tangentă buclei interioare. Rezultă că tangentele în punctul dublu z4 au pantele $\small\pm\sqrt{3}$.

Generarea curbei printr-un program MetaFont

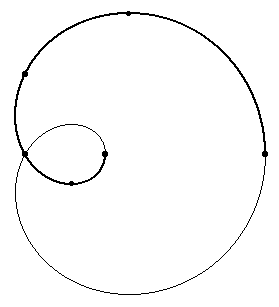
Programul redat mai jos a produs imaginea alăturată aici. Arcul îngroşat se suprapune exact (sau mai prudent, indiscernabil) peste o porţiune din curba trasată cu linie subţire.
Curba subţire a fost trasată "obişnuit": am considerat punctele cercului unitate distanţate între ele cu câte o fracţiune de grad (aici, cu 0.5°) şi le-am aplicat transformarea $\small z(z+1)$, plotând apoi cele (măcar) 720 de puncte rezultate astfel.
În schimb, pentru arcul îngroşat am indicat doar cele 6 puncte marcate pe figură şi direcţiile tangentelor în aceste puncte; pe baza acestor indicaţii, MF a completat arcul respectiv prin mecanismul de interpolare specific.

screen_rows := 600; 
def scaleandshift = scaled 80 shifted (100, 0) enddef;

vardef limax(expr Z) = Z zscaled (Z + right) enddef;  % = z(z+1), z=x+iy

pair k[];
for fi=0 step 0.5 until 360:  % step .25
    k[fi] := limax((cosd fi, sind fi));
endfor
path lmc;
lmc := k[0] for i=0 step .5 until 360: ..k[i] endfor ..k[360];
pickup pencircle; draw lmc scaleandshift;

z1 = ((-1+sqrt(33))/16, sqrt((207+33*sqrt(33))/2)/8);
z2 = ((-1-sqrt(33))/16, sqrt((207-33*sqrt(33))/2)/8);
z3 = z2 reflectedabout((0,0), (2,0));
pickup pencircle scaled .15pt;
for z = (2,0), z1, (-1,1), (-1,0), z3, (0,0): 
    drawdot(z scaleandshift); 
endfor

path p;
atan2 = angle(1, 2) + 180;
p := (2,0){up}..z1{left}..(-1,1){dir atan2}..(-1,0)..z3{right}..{up}(0,0);
pickup pencircle scaled .05pt; draw p scaleandshift;

showit;

Am folosit aceleaşi puncte ca în programul R precedent; dar acum (nefiind explicitată vreo unitate de măsură, în termenii specifici lui MF), coordonatele sunt măsurate în mod implicit în pixeli. Contururile ar apărea mult mai mici decât ne-am dori şi de aceea, am înfiinţat la început macro-ul scaleandshift; de exemplu draw (0,0)--(2,0) ar fi trasat un segment cu lungimea de 2 pixeli, în timp ce draw (0,0)--(2,0) scaled 50 trasează un segment de 100 pixeli.
scaleandshift prevede o mărire de 80 de ori şi o translaţie spre dreapta cu 100 de pixeli (încât porţiunea imaginii finale aflată în stânga originii fixate de către MF să "încapă" în fereastra grafică - v. [1]-IV, la sfârşit); pentru ca imaginea să încapă şi pe verticală, am mărit la 600 (s-a dovedit suficient) numărul de linii orizontale din variabila internă screen_rows.

În prima parte a programului ne-am ocupat de conturul subţire. Întâi, am înfiinţat funcţia limax(z), prin care punctul z văzut ca număr complex este transformat (prin operatorul zscaled) în z(z+1). Am aplicat transformarea limax() punctelor cercului unitate (cos φ, sin φ), crescând φ de la 0° la 360° cu pasul 0.5° şi am înlănţuit punctele rezultate într-o structură de tip path pe care am înscris-o (prin draw şi scaleandshift) în "currentpicture" (structură de date menţinută de către MF, al cărei conţinut va fi afişat în fereastra grafică prin comanda finală showit); am adăugat apoi (prin scaleandshift şi drawdot) cele 6 puncte menţionate la început.

În a doua parte, am constituit o variabilă de tip path din aceste 6 puncte, folosind operatorul de interpolare ".." (denumit de MF "path_join"); conturul respectiv pleacă din punctul (2,0) având aici tangentă verticală îndreptată în sus, ajunge în z1 (punctul cel mai înalt al curbei) cu tangentă ori­zontală, apoi în punctul (-1,1) în care tangenta are panta 2, ş.a.m.d. Prin angle() am obţinut valoarea în grade a pantei 2 şi am adăugat 180° având în vedere sensul de mişcare a peniţei… Rezultă în final conturul îngroşat din imaginea redată mai sus, contur care se suprapune celui subţire (pe porţiunea care conţine cele 6 puncte marcate) obţinut în prima parte a programului.

Simetrizând faţă de axa orizontală conturul îngroşat (adăugând draw p reflectedabout((0,0), (2,0)) scaleandshift;) - vom obţine întreaga curbă.

Constituirea unui simbol corespunzător curbei

În [1] am constituit un font conţinând 5 simboluri; adăugăm în mnemonics.sty declaraţia:

\DeclareMathSymbol \limax {\mathord}{mnem}{"02}

şi adăugăm în monics.mf definiţia de caracter următoare:

beginchar(2, 2.5ht#, 2ht#, 1dp#);  %% Pascal trisectrix
    u := .75u;  % unitatea de măsură (iniţial, u# = 20pt#; v.[1])
    z1 = ((-1+sqrt(33))/16, sqrt((207+33*sqrt(33))/2)/8)*u;
    z2 = ((-1-sqrt(33))/16, sqrt((207-33*sqrt(33))/2)/8)*u;
    z3 = z2 reflectedabout((0,0), (2,0));
    path p;
    atan2 = angle(1, 2) + 180;
    p := (2u,0){up}..z1{left}..(-1u,1u){dir atan2}..(-1u,0)..z3{right}..{up}(0,0);
    pickup path_pen;  % v. [1]
    draw p shifted(1.2u, 0);
    draw p reflectedabout((0,0), (2,0))  shifted(1.2u, 0);
    currentpicture := currentpicture shifted(0, 1u);  % urcă "axa matematică"
endchar;

În această definiţie doar am copiat partea a doua din programul anterior (conturul prin cele 6 puncte - cel îngroşat pe figura de mai sus) şi am simetrizat conturul respectiv faţă de axa orizontală; în plus, am scalat coordonatele printr-o anumită unitate de măsură (plecând de la aceea considerată iniţial în monics.mf) şi am reglat puţin (folosind shifted) poziţionarea orizontală şi cea verticală, în cadrul boxei asociate caracterului.

Pentru o testare imediată, putem adăuga în fişierul "simplu.test" din [1] linia următoare:

\smallskip  Pascal $\limax$ trisectrix

Apoi, pdflatex simplu.test (din linia de comandă) va produce un fişier PDF în care pe lângă cele 5 caractere prevăzute anterior în "simplu.test", apare şi caracterul tocmai definit mai sus:

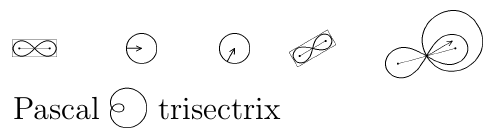
Axa orizontală (sau "axa matematică") este la acelaşi nivel ca în cazul primelor 4 simboluri, iar încadrarea faţă de textul împrejmuitor pare destul de bună. Dar putem încă experimenta (căutând dimensionări şi delimitări mai bune), modificând în principal unitatea de măsură considerată (şi alţi parametri, de exemplu valorile din shifted).