Expresii și arbori

Următoarea funcție produce (după un algoritm recursiv clasic, descris în multe locuri) toate permutările unui vector dat:

bind_perm <- function(W) { # cu W=1:n, sau W=c(...)
    P <- NULL
    k <- length(W)
    if(k == 1) return(W)
    for(i in 1:k)
        P <- rbind(P, cbind(W[i], bind_perm(W[-i])))
    P  # matricea permutărilor vectorului (pe linii)
}

Mai jos vom avea nevoie de permutările "cu repetiție", pentru două valori '0' împreună cu două valori '1' (din tidyverse avem `%>%`, dplyr::distinct(), etc.):

> Mp <- bind_perm(c(0, 0, 1, 1)) %>% as.data.frame() %>% distinct()
    1    0  0  1  1
    2    0  1  0  1
    3    0  1  1  0
    4    1  0  0  1
    5    1  0  1  0
    6    1  1  0  0

Vizăm arborii aritmetici cu 3 operatori binari dintre cei patru obișnuiți ('+', '-', '*', '/') și cu 4 operanzi. Rădăcina arborelui și deasemenea, rădăcina fiecărui subarbore este un operator; indexând nodurile de sus în jos și pe fiecare nivel de la stânga spre dreapta, nodurile 6 și 7 sunt sigur, operanzi (și rămân de elucidat 4 noduri).

Desemnăm prin '1' un operator oarecare și prin '0' un operand oarecare; parcurgând cele 7 noduri în ordinea prefixată (rădăcină și recursiv, subarborele-stâng, apoi cel drept), avem deocamdată, această exprimare parțială a arborelui respectiv:

    index:  1 2 3 4 5 6 7
      nod:  1 _ _ _ _ 0 0

În cele 4 poziții 2:5 avem de pus doi de '0' și doi de '1' — deci câte una dintre cele 6 combinații redate mai sus în matricea Mp. Dar cu siguranță, prima combinație "0 0 1 1" trebuie exclusă: arborele a cărui descriere-prefix începe cu "1 0 0" nu poate fi extins (fiindcă rădăcina fiecărui sub-arbore trebuie să fie un operator); celelalte 5 combinații, prefixate cu '1' și sufixate cu '00', ne-ar da descrierile-prefix ale arborilor respectivi:

Pr5 <- lapply(2:6, function(i) 
    paste0("1", paste0(Mp[i, ], collapse = ""), "00", collapse = ""))
[[1]]  "1010100"
[[2]]  "1011000"
[[3]]  "1100100"
[[4]]  "1101000"
[[5]]  "1110000"

Este interesant de observat că descrierile-prefix permit și unele comparări între arborii respectivi; în Pr5[[1]], fiecare nod '1' are un fiu-stâng '0' (iar ultimul '0' este fiu-drept), iar în Pr5[[5]] fiecare nod '1' are un fiu-drept '0' (iar un '0' este fiu-stâng) — încât, deducem că arborii corespunzători acestor două descrieri-prefix sunt simetrici!

Funcția derive_canon() de mai jos, pleacă de la observația că U = '100' apare ca subșir în descrierea-prefix a oricărui arbore aritmetic, iar aceasta are forma parantezată U = 1(0,0); cu înlocuire, Pr5[[1]] de exemplu, devine "1010U"; apoi, V = '10U' are forma parantezată "V = 1(0,U)" și obținem "10V"; înlocuind înapoi pe 'V' în 1(0, V), apoi și pe 'U' — rezultă forma prefix parantezată a arborelui respectiv, 1(0,1(0,1(0,0))) (cu care am putea vizualiza arborele respectiv, prin funcția toDOT() din [1]…).

derive_canon <- function(PX) {  # formă prefix (cu '1' și '0') de arbore aritmetic
    derive <- function(OLR)  # șir "1.." unde '.' este '0' sau '1'
        sub("(.)(.)(.)", "\\1\\(\\2,\\3\\)", OLR)  # produce "1(.,.)"
    P1 <- PX %>% gsub("100", "U", .) %>%
                 gsub("10U", "V", .) %>%
                 gsub("1U0", "W", .) %>% derive(.)
    P1 %>% str_replace_all(., "W", derive("1U0")) %>%
           str_replace_all(., "V", derive("10U")) %>%
           str_replace_all(., "U", derive("100"))
}

Obținem expresiile prefix parantezate ("canonice") pentru formele-prefix din Pr5:

AR <- map(Pr5, derive_canon)
    [[1]]  "1(0,1(0,1(0,0)))"
    [[2]]  "1(0,1(1(0,0),0))"
    [[3]]  "1(1(0,0),1(0,0))"
    [[4]]  "1(1(0,1(0,0)),0)"
    [[5]]  "1(1(1(0,0),0),0)"

Următoarea funcție produce matricea muchiilor arborelui, folosind forma canonică rezultată mai sus (imitând desigur, funcția toDOT() din [2]):

edges_matrix <- function(E_prefix) {
    EDG <- matrix(0, nrow = 6, ncol = 2, byrow = TRUE)
    Es <- strsplit(E_prefix, "")[[1]]
    root <- 1
    g <- 1
    for(i in 1:length(Es)) {
        nod <- Es[i]
        switch(nod,
            '(' = { root <- root * 2
                    EDG[g, ] <- c(root %/% 2, root)
                    g <- g + 1
                  },
            ',' = { root <- root + 1
                    EDG[g, ] <- c(root %/% 2, root)
                    g <- g + 1
                  },
            ')' = { root <- root %/% 2 },
        )
    }
    EDG
}    

E drept că… parcă nu obținem ce ar trebui:

> edges_matrix(AR[[2]])
     [,1] [,2]
[1,]    1    2
[2,]    1    3
[3,]    3    6  # (?) muchia corectă ar fi probabil, 3--4
[4,]    6   12  # ??
[5,]    6   13  # ??
[6,]    3    7

Am încercat un timp (și nu-i simplu), să "corectăm" în edges_matrix(), calculul de muchii (preluat oarecum mot à mot, din funcția anterioară toDOT()) — dar de fapt, intenționând de la bun început, să vizualizăm arborii respectivi prin pachetul igraph (și nu prin fișiere DOT), corectarea este chiar inutilă!
Funcția igraph::delete_vertices() ne va permite să eliminăm vârfurile izolate (vârfurile 11, 10, chiar 5 și altele, nu sunt capete ale vreunora dintre muchiile redate mai sus — deci sunt vârfuri izolate ale grafului din care face parte arborele respectiv); iar frumusețea (de așteptat, desigur) este că vârfurile rămase în urma operației de eliminare sunt re-notate automat cum se cuvine, cu 1:7.

Secvența următoare construiește și afișează într-o fereastră grafică, arborii listați (în format prefix parantezat) în lista AR:

library(igraph)
opar <- par(mfrow = c(2, 3), mar = c(1, 0, 0, 0) + 0.1, font = 2,
            bty = "n", xaxt = "n", yaxt = "n")  # parametri grafici
for(i in c(1, 5, 3, 2, 4)) {  # parcurgem lista AR într-o anumită ordine...
    EG <- edges_matrix(AR[[i]])
    g <- graph_from_edgelist(EG, directed = FALSE)
    vd <- V(g)[which(degree(g) == 0)]
    G <- delete_vertices(g, vd)
    V(G)$color <- ifelse(degree(G) > 1, "lightgray", "white")
    coords <- layout_as_tree(G, root = 1)  # coordonatele nodurilor
    plot(G, layout = coords) 
    mtext(paste0(Pr5[[i]], collapse=""), side = 1, line = -2)
}
par(opar)  # restaurează parametrii grafici inițiali

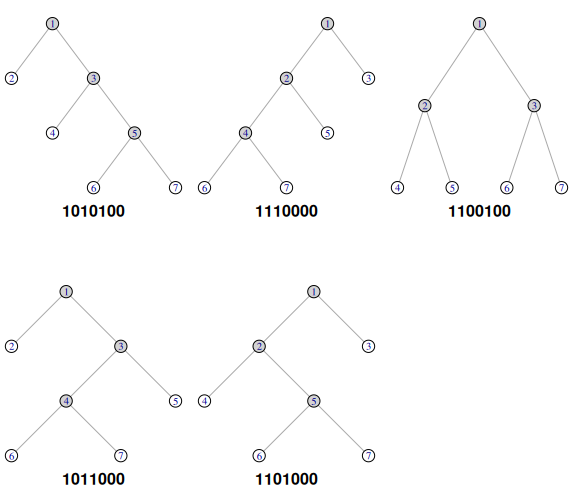
Nodurile corespunzătoare operatorilor '1' au fost colorate (cu lightgray); dedesubtul fiecărui arbore am însemnat notația-prefix a lui (în termenii '1' și '0').
Se observă desigur, că primii doi arbori — AR[[1]] și AR[[5]] — și respectiv, ultimii doi (AR[[2]] și AR[[4]]) sunt simetrici unul față de celălalt.

Nota bene. Bineînțeles că la fel ca mai sus, putem trata și expresiile aritmetice cu mai mult de trei operatori…

… ce interes pot avea arborii aritmetici?!

Să se demonstreze că nu există expresii aritmetice de valoare 24, formate cu 3 operatori obișnuiți și cu operanzii 3, 4, 6 și 7.

Încercările obișnuite de a forma o asemenea expresie au eșuat, încât ne-am pus problema să "demonstrăm" că nu există soluții; ar fi chiar surprinzător, un raționament coerent, fluent și scurt — dar nu reușim să-l vedem, rămânându-ne doar ideea (exploatată mai demult și în [2]) de a genera și evalua toate expresiile posibile pe operanzii dați, pentru a vedea dacă găsim una de valoare 24…
Desigur… "altă întrebare": de ce să fie interesantă valoarea 24, în loc de 25 de exemplu?! Păi e "după facultăți" (cum zicea unul din Siliștea lui Marin Preda); cât este numărul de ore ale unei zile? câte "grand-slamuri" a câștigat (deocamdată) Djokovici? Câte permutări sunt, pentru 4 elemente distincte? Sau și așa: subgraful celor 48 de vârfuri exterioare centrului lărgit al tablei de șah, adicența fiind dată de mutarea calului, este format din două drumuri disjuncte de lungime 24.
(am răspuns la "întrebare"?)

Deci povestea noastră continuă: folosim cei 5 arbori evidențiați mai sus, în forma prefix-parantezată din lista AR, pentru a genera toate expresiile cu 3 operatori obișnuiți și cu 4 operanzi (trăgând apoi concluziile pentru operanzii 3, 4, 6, 7 — poate fi și asta, o "demonstrație" de ce nu, doar că… nu prea are farmec).

Intern, R lucrează cu "S-expresii" (forme prefix-parantezate; v. [1]) și doar pentru afișare, folosește forma infixată obișnuită; de exemplu, expresia infixată "a+b" are intern, forma funcțională "`+`(a,b)".
Funcția următoare înlocuiește '1' și '0' din expresia prefix-parantezată a unui arbore aritmetic (de 7 noduri), cu operatorii și operanzii specificați în vectorii de tip character 'opr' și respectiv 'var'; dar operatorii trebuie indicați folosind backtick (accent grav), de exemplu "`*`" (care va fi interpretat ca "apel de funcție") și nu simplu "*".

derive_expr <- function(Arb, opr, var) {
    str_replace(Arb, "1", opr[1]) %>%
    str_replace(., "1", opr[2]) %>%
    str_replace(., "1", opr[3]) %>%
    str_replace(., "0", var[1]) %>%
    str_replace(., "0", var[2]) %>%
    str_replace(., "0", var[3]) %>%
    str_replace(., "0", var[4])
}

str2lang() analizează expresia (listând-o intern în forma prefix-parantezată; v. [1]) și dacă este cazul de afișare, o afișează în formă infixată; eval produce valoarea expresiei (pe baza formei prefix-parantezate a acesteia). De exemplu:

> DE <- derive_expr(AR[[1]], opr = c("`*`", "`+`", "`-`"),
                             var = as.character(c(2,3,4,5))) %>% print()
    [1] "`*`(2,`+`(3,`-`(4,5)))"
> str2lang(DE)
    2 * (3 + (4 - 5))  # afișează în formă infixată
> eval(str2lang(DE))  # 4  (valoarea expresiei)

În cazul de față, expresia este deja în forma prefix-parantezată, numai că este totuși un "șir de caractere"; str2lang() transformă șirul respectiv în listă (cu sub-liste) de "simboluri" funcționale (v. [1]).

Definim vectorul operatorilor, formăm prin expand.grid() tabelul tuturor permutărilor de câte 3 operatori dintre cei 4 și calculăm numărul N al expresiilor posibile:

operators <- c("`+`", "`-`", "`*`", "`/`")  
Bin2 <- expand.grid(rep(list(operators), 3), stringsAsFactors = FALSE)
N <- nrow(Bin2) * length(AR) * 24  # numărul total de expresii (7680)

Cu cele de mai sus, următoarea funcție produce un vector care conține toate expresiile posibil de format cu operatorii și operanzii indicați:

arithExpr <- function(operands = as.character(c(3, 4, 6, 7))) { 
    operms <- bind_perm(operands)
    VE <- vector("character", N) 
    nr <- 1
    for(j in 1:length(AR)) 
        for(h in 1:nrow(operms)) 
            for(k in 1:nrow(Bin2)) {
                VE[nr] <- derive_expr(AR[[j]], 
                              as.character(Bin2[k, ]), operms[h, ])
                nr <- nr + 1
            }
    VE
}

Găsim (cam în 7-8 secunde) cele 7680 de expresii și aplicăm str2lang() și eval() pe vectorul respectiv; apoi, selectăm expresiile cu valoarea dorită:

prnTime(" ")
AE <- arithExpr()
prnTime("\n")  # 7 sec.
vAE <- sapply(sapply(AE, str2lang), eval) %>% as.vector()
v24 <- which(vAE == 24)
sapply(AE[v24], str2lang) %>% print()

Pentru valoarea 24 se afișează în final "named list()", adică nu există expresii aritmetice pe operanzii (3, 4, 6, 7), cu valoarea 24 — ceea ce încheie "demonstrația". Desigur, putem modifica puțin operatorii; dacă implicăm "`%/%`", adică "împărțirea întreagă" în loc de cea obișnuită, obținem 24 prin "(7%/%4 + 3) * 6", etc.

Bineînțeles că arithExpr() poate fi apelată cu oricare alți 4 operanzi din mulțimea cifrelor 1:9; iar unele idei de studiu statistic al valorilor tuturor expresiilor formate, avem mai demult în Expresii aritmetice în R…