introducere...

În limbajul R analiza sintactică a expresiilor este în bună măsură, transparentă (chiar fără vreun pachet specializat); n-ar fi necesar, dacă am avea de văzut, din cine știe ce motive, arborele sintactic sau poate forma prefixată a unei expresii, n-ar fi necesar să creem întâi un model de arbore, specializat pe o gramatică obișnuită a expresiilor (cum s-ar impune în cazul limbajului C, v. [2]).
Intern, R operează cu "S-expresii" (numai aparent, "neparantezate"), încât explorarea care urmează (vizând totuși expresii aritmetice) ar fi valabilă pentru orice expresie R (se cuvine de știut că o S-expresie ("Symbolic expression") este o reprezentare textuală liniară, parantezată, a structurilor arborescente). De exemplu, o instrucțiune ca "for(i in 1:10)" este de fapt o S-expresie cam ca "(`for`, i, `:`(1,10))".

Pentru o expresie aritmetică obișnuită (indicată în argumentul text), parse() — cel mai obișnuit instrument de analiză sintactică, pus la dispoziție chiar de pachetul base — produce un obiect clasat ca "expression" (sau poate în unele contexte, "language"):

> E <- "a / (b - c/d)"  # o expresie aritmetică oarecare
( Lr <- parse(text = E) )  # > class(Lr) [1] "expression"
expression(a / (b - c/d))  # Lr[1]
> Lr[[1]]  # conținutul listei Lr[1]
a/(b - c/d)  # Nu "șir de caractere", ci simboluri și... apeluri

De fapt, se construiește o listă care conține până la urmă componentele sintactice ale expresiei respective, înlănțuite în ordinea impusă de gramatica limbajului; această "listă" poate fi investigată la fel cu listele obișnuite, folosind în principal operatorul '[['. Baza Lr[[1]] a acestei liste este expresia respectivă, în forma "brută" (simboluri și '('); Lr[[1]] acoperă ea însăși o listă, cu un anumit număr de componente:

> length(Lr[[1]])
[1] 3  # Lr[[1]] are 3 componente
> Lr[[1]][[1]]
`/`  # operator (sau "apel")
> Lr[[1]][[2]]
a  # primul operand (argument al apelului)
> Lr[[1]][[3]]
(b - c/d)  # al doilea operand (o sub-expresie)

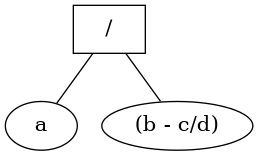
Cele trei componente ale lui Lr[[1]] sunt "înlănțuite" în ordine prefixată (operator, primul operand, al doilea operand); subliniem că R afișează expresiile în forma infixată obișnuită utilizatorului, dar intern folosește formatul prefixat: `/`(a, (b-c/d)) (unde subexpresia "b-c/d" trebuie tradusă și ea, în forma prefixată).

Tocmai fiindcă analiza sintactică pleacă de la Lr[[1]] (conținutul listei Lr[1]), s-a constituit o "scurtătură" str2lang(E), pentru parse(text=E)[[1]]:

> Lr <- str2lang(E)  # tocmai rezultatul "Lr[[1]]" dat prin parse() mai sus
> sapply(as.list(Lr), length)  # [1] 1 1 2

Aplicând length() pe cele trei componente din Lr (evidențiate direct mai sus), vedem că pentru subexpresia rămasă de analizat avem două componente:

> Lr[[3]][[1]]
`(`  # operatorul de "apelare"
> Lr[[3]][[2]]
b - c/d  # "operandul" apelului (acum, o sub-expresie)

Cu alte cuvinte, subexpresia "(b-c/d)" are forma internă obișnuită pentru funcții,
`(`(b-c/d) — unde `(` este o funcție: class(`(`) ne dă [1] "function". Desigur, putem continua așa, din aproape în aproape, pentru a "traduce" și subexpresia rămasă…

Dar putem proceda (desigur!) mai concis, pentru a obține (în formă liniară) întregul arbore sintactic asociat expresiei (presupunând, că am avea nevoie de întregul arbore).
Parcurgând Lr "din aproape în aproape", am văzut mai sus că întâlnim fie operatori, fie operanzi obișnuiți ai acestora, fie… "subexpresii" (pentru care ar trebui să reluăm parcurgerea din aproape în aproape); putem stabili că s-a întâlnit o subexpresie și nu un operator sau operand obișnuit, folosind is.call():

> is.call(str2lang("b-c/d"))  # pentru "subexpresii"
[1] TRUE
> is.call("c")  # pentru operanzi obișnuiți
[1] FALSE

Prin urmare, n-avem decât să parcurgem recursiv Lr, "reapelând" dacă întâlnim o componentă pentru care is.call() indică TRUE; iar dacă lungimea listei asociate componentei curent întâlnite este 1, atunci să afișăm valoarea respectivă:

get_ast <- function(L) {
    if(length(L) == 1) print(L)
    purrr::map_if(as.list(L), is.call, get_ast)
}

> get_ast(str2lang(E))
[[1]]
`/`
[[2]]
a
[[3]]
[[3]][[1]]
`(`  # apelează calculul de sub-expresie
[[3]][[2]]
[[3]][[2]][[1]]
`-`
[[3]][[2]][[2]]
b
[[3]][[2]][[3]]
[[3]][[2]][[3]][[1]]
`/`
[[3]][[2]][[3]][[2]]
c
[[3]][[2]][[3]][[3]]
d

Dar să observăm că nu ar fi fost necesar să afișăm "valorile", reducând funcția la:

get_ast <- function(L)
    purrr::map_if(as.list(L), is.call, get_ast)

Astfel, prin str() putem reda mai simplu și mai clar (cu ierarhizare) "valorile" respective (fără indecși expliciți de subliste, cum aveam mai sus):

> AST <- get_ast(str2lang(E))  # "Abstract Syntax Tree"
> str(AST)
List of 3  # expresie
 $ : symbol /  # rădăcină
 $ : symbol a  # subarborele stâng
 $ :List of 2  # sub-expresie (subarborele drept)
  ..$ : symbol (
  ..$ :List of 3  # sub-sub-expresie (sub-subarbore stâng)
  .. ..$ : symbol -
  .. ..$ : symbol b
  .. ..$ :List of 3  # sub-sub-sub-expresie
  .. .. ..$ : symbol /
  .. .. ..$ : symbol c
  .. .. ..$ : symbol d

Mai mult, să observăm că putem reda liniar structura arborescentă AST, aplicându-i recursiv — prin rapply(), cu argumentul how="unlist" — funcția as.character():

> ( Prf <- rapply(AST, as.character, how = "unlist") )
[1] "/" "a" "(" "-" "b" "/" "c" "d"

Excluzând `(` (care nu este un "simbol", ci un "apel de funcție"), am obține forma prefixată (propriu-zisă, neparantezată) a expresiei:

> Prf[-3] |> paste0(collapse = " ")  # intercalăm " ", pentru lizibilitate
[1] "/ a - b / c d"  # forma prefixată (neparantezată) a expresiei

Ar fi poate cazul, să amintim (v. [2]) că și în Prolog putem obține (cu redare imediată) forma prefixată — și parantezată — a unui termen-expresie:

vb@Home:~/25iun$ swipl -q
?- write_canonical(a/(b-c/d)).
/(a,-(b,/(c,d)))  % forma prefixată parantezată ("canonică")
true.

Avantajul parantezării (dincolo de considerente mai profunde) ar fi acela că permite un algoritm foarte simplu (v. [3]) pentru a obține o descriere DOT a arborelui sintactic — permițând vizualizarea grafică (arborescentă) a expresiei respective.

În treacăt, să observăm că în învățământul gimnazial se folosesc în mod tacit, atât "S-expresii" (… când se aplică regula "calculează întâi sub-expresia din paranteza cea mai interioară"), cât și reprezentări grafice arborescente (ca acelea descrise prin DOT), de exemplu pentru "analiza sintactică și morfologică a frazei"… Doar că lucrurile rămân mereu la nivelul de "reguli" (expuse, însușite și aplicate mecanic) și nu se leagă!

Obținerea formei prefixate canonice

Pentru a deduce, din rezultatul dat de str2lang(), forma prefixată canonică a expresiei, ar fi suficient să închidem parantezele, inserând ')' unde se cuvine.

Dar să regrupăm întâi funcțiile de mai sus și să considerăm pentru diverse ilustrări, o expresie mai complicată:

R_prefix <- function(E_infix) {
    get_ast <- function(L)
        purrr::map_if(as.list(L), is.call, get_ast)
    rapply(get_ast(str2lang(E_infix)), as.character, how = "unlist") |>
        paste0(collapse = "")
}
E <- "(a + b / c)*((d - e)/(f + g - h))"
Px <- R_prefix(E)  # [1] "*(+a/bc(/(-de(-+fgh"

De observat întâi, că expresia E conține paranteze inutile… În general, sensul pentru care considerăm expresiile este dat de evaluarea acestora, iar E echivalează cu expresia fără paranteze inutile "(a + b / c)*(d - e)/(f + g - h)" (având în vedere că operatorii '*' și '/' au aceeași prioritate). Iar pe de altă parte, "canonic" ar trebui să însemne, în primul rând, "fără paranteze inutile"…
Totuși, cam la fel cu faptul că în diverse limbaje, anumite paranteze "inutile" delimitează un bloc (cu reguli specifice de evaluare) — și în cazul de față parantezele inutile pentru evaluare, existente în E, arată o anumită formă a expresiei:

Px nu este "forma prefixată", fiindcă (spre deosebire de cazul anterior) am păstrat cele 4 paranteze '(' care pentru R semnifică operatorul de apel ("call"); aceste paranteze indică în fond unde încep sub-expresiile (sau "blocurile" și sub-blocurile) avute în vedere, încât putem deduce unde trebuie să inserăm și ')', pentru a ajunge la forma prefixată parantezată ("canonică").
Anume, fiecare bloc este cuprins între câte două caractere '(' consecutive, sau între ultimul '(' și sfârșitul expresiei; deci ar trebui să inserăm ')' după fiecare bloc, astfel: *(+a/bc)(/)(-de)(-+fgh) — urmând apoi să vedem cum exprimăm "prefix-canonic" fiecare sub-bloc (de exemplu, "-de" va trebui scris ca "-(d,e)", evidențiind operatorul-rădăcină "-" și operanzii-subarbori "d" și "e").

Noi am făcut inserțiile și înlocuirile respective aplicând de câteva ori (din aproape în aproape) gsub(), lucrând cu "expresii regulate"; de exemplu:

Qx <- gsub("(\\([^\\(]+)", "\\1)", Px)  # adaugă ')' după fiecare sub-bloc
    [1] "*(+a/bc)(/)(-de)(-+fgh)"

dar cu siguranță că se poate închega un program mai "curat" (și care să vizeze orice expresie)… Rezultatul final, reprezentând forma prefixată canonică a expresiei E de mai sus este "*(+(a,/(b,c)),/(-(d,e),-(+(f,g),h)))".

Descrierea DOT a arborelui sintactic

Următoarea funcție modelează în R algoritmul prezentat în [3], considerând că expresia indicată este în formă prefixată parantezată (fără spații), operanzii fiind indicați prin litere (și având ca operatori pe cei patru obișnuiți):

toDOT <- function(E_prefix, File) {
    sink(File)  # fișierul în care va scrie cat()
    cat("# ", E_prefix, "\n")
    cat("graph AST {\n")
    cat("node[shape=plaintext, fontsize=16]\n")
    Es <- strsplit(E_prefix, "")[[1]]  # despărțim caracterele, într-un vector
    root <- 1  # indexăm nodurile arborelui, în preordine
    for(i in 1:length(Es)) {
        nod <- Es[i]
        if(nod %in% letters) {  # operand
            cat(root, '[label="', nod, '"]\n')
            next()
        }
        switch(nod,
            '(' = { root <- root * 2  # muchia spre stânga
                    cat((root %/% 2), "--", root, "\n")
                  },
            ',' = { root <- root + 1  # muchia spre dreapta
                    cat((root %/% 2), "--", root, "\n")
                  },
            ')' = { root <- root %/% 2 },
            cat(root, '[label="', nod, '", shape=square]\n')  # operator
        )
    }
    cat("}")  # încheie descrierea AST
    sink()  # închide fișierul, reorientând normal scrierea
    return(invisible())
}    

Ep <- "*(+(a,/(b,c)),/(-(d,e),-(+(f,g),h)))"
toDOT(Ep, File = "Ep.dot")

Lansând asupra fișierului rezultat "Ep.dot", programul dot (cu opțiunea "-Tpng") — obținem imaginea PNG a arborelui sintactic al expresiei respective:

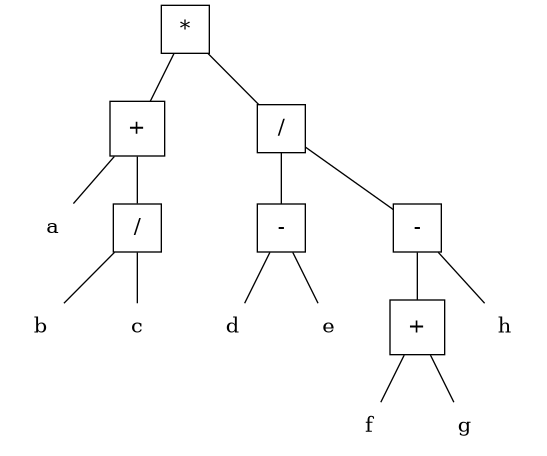
… iar pentru gimnaziști ar deveni evident sau în orice caz mai clar, cum să evaluăm expresia: parcurgem arborele de jos în sus, calculând mereu câte o "cea mai interioară paranteză" la momentul respectiv și substituind apoi rădăcina acesteia, cu valoarea rezultată (apoi urcăm pe nivelul următor și repetăm).

Observație vizând practica de evaluare

R_prefix(E) transformă expresia în forma care putem zice că este "nativă pentru R", cu `(` ca prefix pentru sub-expresii: "*(+a/bc(/(-de(-+fgh" — și nu se poate să nu observăm că această formă (de la care am derivat mai sus, întregul arbore sintactic) este de fapt, cea mai convenabilă pentru procesul practic de evaluare concisă a expresiei!

Aici, variabilele implicate (presupuse a fi cu valori numerice) sunt independente între ele, astfel că evaluarea lui E poate decurge evaluând pe rând (în niște variabile auxiliare) sub-blocurile indicate de '(':

α = "+a/bc" = a + b/c  # valoarea numerică a sub-expresiei
β = "-de" = d - e
γ = "-+fgh" = f + g - h

După obținerea rezultatelor α,β,γ, expresia E revine la "* α (/β γ"; evaluăm sub-blocul δ = "/β γ" = β/γ și calculul se reduce la "* α δ" — deci E are valoarea α*δ.