Considerăm familia de curbe (plane) definită de ecuația:

Pentru $m=0$ avem cercul unitate, plus un punct izolat $(0,0)$; când $m$ crește spre $m=0.5$, cercul inițial se deformează în partea de sus, rămânând însă un oval convex (plus punctul izolat $(0,0)$); apoi, crescând spre $m=1$, ovalul respectiv capătă o adâncitură netedă. Când $m=1$ obținem o cardioidă cu nodul în origine (care acum este punct singular); pentru $m > 1$ rezultă câte un limaçon ("melcul" lui Pascal).
Următoarele panouri grafice sintetizează aceste observații asupra ecuației (1):

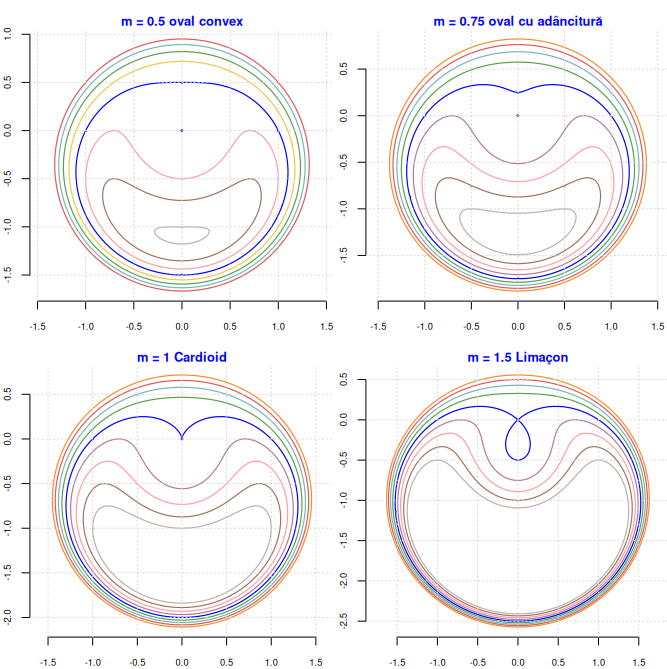
Culoarea "blue" arată curbele $f_{\mathrm{m}}(x,y)\boldsymbol{=0}$; cu alte culori am asociat în fiecare caz, câteva curbe de nivel $f_{\mathrm{m}}(x,y)\boldsymbol{=\lambda}$ (cu $\lambda\ne 0$, de la $-1$ spre $1$ cu pasul $0.25$).

Pentru a produce această figură am folosit pachetul plotlev din [1], aducându-i cu acest prilej două îmbunătățiri (constând în eliminări).
Am eliminat din plot_contours() apelul plot.new(), din cauza căruia plotarea în cele 4 panouri (constituite folosind par(mfrow(2,2))) eșuează (mai precis, rezulta o fereastră conținând numai prima coloană de panouri, apoi o a doua care o acoperea pe prima, pentru a doua coloană de panouri).
În col2lev() am înlocuit colorarea aleatorie a curbelor de nivel, adoptând în loc setul "Tableau 10" plus "Blue" pentru nivelul 0: (pentru investigări asupra unor funcții exprimate analitic sunt suficiente patru-cinci niveluri; am prevăzut totuși un gray50, pentru nivelurile >10, dacă s-au indicat).

După aceste modificări în plotlev, următorul program produce figura de mai sus:

library(plotlev)
FUN <- function(x, y)  # o familie de curbe (de parametru m)
    (x^2 + y^2 + m*y)^2 - (x^2 + y^2)  # = 0
P <- c(0.5, 0.75, 1, 1.5)  # valori pentru parametrul m
X <- Y <- seq(-3, 3, by = 0.01)  # (?) pentru toate panourile (?)
lbl <- c("oval convex", "oval cu adâncitură", "Cardioid", "Limaçon")
opar <- par(mfrow = c(2,2), mar = c(2,2,2,0), bty="n")
for(m in P) {
    Z <- outer(X, Y, FUN)
    H <- contourLines(X, Y, Z, levels = seq(-1, 1, by=0.25))
    plot_contours(H, lwd = 1.2, cex.axis = 0.7)
    mtext(paste("m =", m, lbl[match(m, P)]), 
          side = 3, cex = 0.8, font = 2, col="blue")
    grid()
}
par(opar)  # reconstituie la valorile implicite, parametrii grafici

Avem de făcut o serie de observații, asupra acestui program…

În primele două panouri este marcat punctul izolat $(0,0)$ (toate curbele $f_{\mathrm{m}}$ trec prin origine); dar dacă pentru X și Y indicam drept capete nu ±3, ci de exemplu ±π (sau alte valori iraționale) — atunci originea ar fi scăpat marcării: cu pasul considerat, de o sutime (sau o miime), originea n-ar mai fi fost găsită în vectorul Z, ca punct al curbei… (dar aceasta ar fi o "falsă problemă": înainte de a aplica outer() pentru a găsi Z, prin X <- c(X, 0.0) puteam adăuga originea, sau vreun alt punct izolat, vectorilor inițiali X și Y).

Curbele $f_{\mathrm{m}}$ au $Oy$ ca axă de simetrie, deci ordonatele punctelor lor variază într-o plajă care se lărgește odată cu $\mathrm{m}$; pentru primele două panouri (cu $\mathrm{m}\le 0.75$) era suficient să luăm Y de la $-1.5$ la 1, iar pentru următoarele două, de la $-3$ la 1. Domeniul X crește deasemenea, odată cu $\mathrm{m}$, dar mult mai puțin în comparație cu Y.
Însă în program am ales aceleași divizări X și Y (între $-3$ și $3$) pentru toate cele patru cazuri; dacă alegeam pentru al 4-lea panou, nu $\mathrm{m}=1.5$, ci de exemplu $\mathrm{m}=4$, atunci curba respectivă ar fi fost redată trunchiat (fără punctele cu ordonate mai mici ca $-3$). Considerând X între $-3$ și $3$ — când de fapt, abscisele punctelor curbelor din cele 4 panouri acoperă numai domeniul limitat de $\pm 1.6$ — prin outer() sunt calculate și o groază de puncte $(x, y=f_{\mathrm{m}}(x, y))$ neaflate pe vreuna dintre curbele de nivel din cazul $\mathrm{m}$ respectiv…
Am putea evita acest defect, definind X și Y pentru fiecare caz $\mathrm{m}$ în parte, dar numai dacă am găsi în prealabil o formulă de calcul a limitelor respective (altfel, fără o formulă, ar trebui să plecăm cu X și Y suficient de largi și să aplicăm get_limits() rezultatului întors de outer(), după care să redefinim X și Y conform limitelor găsite și abia apoi să producem graficul prin plot_contours() — ceea ce ar încărca prea urât programul de mai sus; în plus, durata totală a execuției n-ar fi mai mică).

În sfârșit, ar fi de semnalat următorul aspect. Am fi dorit nu patru panouri, ci șase; cele două adăugate ar fi evidențiat că pe măsură ce $\mathrm{m}$ crește (spre infinit), bucla interioară a "melcului" se mărește (iar nodul urcă) — sugerând că la limită, $f_{\mathrm{m}}$ ajunge să coincidă (din nou) cu un cerc…
Însă n-am putut folosi (direct) mfrow(3,2): cele șase panouri nu pot încăpea în "fereastra grafică". Este un bun prilej pentru a ne lămuri: "fereastra grafică" nu ține de ecran, ci mult mai general, de "dispozitivul" ales pentru redarea grafică; putem obține cele 6 panouri într-o pagină PDF (dimensionând-o convenabil) folosind pdf("2602p3.pdf", 10,10) și apoi par(mfrow(3,2)) — urmând ca după plotarea panourilor să închidem dispozitivul, prin dev.off() (care și transferă pe disc, pagina PDF creată astfel).

Subliniem că ne-am ocupat numai "tangențial" de familia de curbe (1), plecând de la observația că parametrul care apare în ecuațiile cardioidei și "melcului" (v. Wikipedia) ar putea să figureze și numai într-un singur loc (în forma (1), numai în termenul "my")… Altfel, aceste curbe sunt printre cele mai cunoscute curbe de gradul IV, încât n-am găsit necesar să facem vreun calcul care să justifice și matematic, observațiile de mai sus asupra familiei acestora.