Pentru a trasa graficul unei funcții $y=f(x)$ (care produce câte o singură ordonată $y$, pentru fiecare abscisă $x\in[a,\,b]$), încă ne putem folosi de această schemă de bază: $\mathrm{for}(x=a; x <= b; x\, +=\, 0.01)\, \mathrm{draw\_point}\,(x, f(x))$ — după ce, lucrând (prin 1985) pe un ZX Spectrum, mai apoi și pe un "PC" cu I80286, treceam ecranul din "mod text" în "mod grafic" (adică astăzi, inițializam "fereastra grafică") și defineam o funcție "draw_point"…; desigur, între timp lucrurile s-au "simplificat" și eventual, putem plota graficul și cu o singură comandă (precum în R, curve(x^3-3*x, -pi, pi)).
Iar dacă aveam de reprezentat grafic curba definită implicit de o funcție $F(x,\,y)$, atunci trebuia să iterăm și după $x$ și după $y\in[c,d]$, plotând punctul $P(x,y)$ pentru toate ordonatele $y$ la care $F(x,y)=0$; într-o formulare "modernă", pentru un cerc:

R <- 0.7
# funcția F(x,y) ale cărei valori zero definesc un cerc de rază R
FUN <- function(x, y) x^2 + y^2 - R^2
# abscisele și ordonatele punctelor cercului (secvențiate cu pasul 0.01)
X <- Y <- seq(-R, R, by = 0.01)
# inițializează fereastra grafică în care se vor plota punctele curbei
plot(0, type="n", xlim = c(-R, R), ylim = c(-R, R), asp = 1)
for(x in X)  # parcurge abscisele
    for(y in Y)  # pentru fiecare abscisă, parcurge ordonatele
        if(abs(FUN(x,y)) < 0.01)  # dacă aparține curbei, plotează P(x,y) 
            points(x, y, pch=16, cex=0.4)

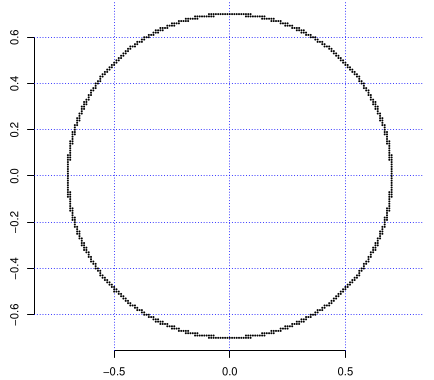
Câteva observații de bun-simț asupra secvenței (și figurii) redate mai sus, ne vor conduce în cele din urmă la formularea într-adevăr "modernă", a lucrurilor…

plot() pretinde niște abscise și niște ordonate — și de regulă va trasa punctele corespunzătoare acestora; de exemplu, dacă am fi constituit în prealabil o matrice "M" conținând coordonatele punctelor cercului, atunci plot(M, asp=1) ar fi plotat deja cercul respectiv (stabilind intern limitele necesare valorilor din "M", dar cu "aspect-ratio"=1, adică având aceeași unitate de măsură pe axe și folosind valorile implicite pentru aspectul și mărimea punctelor).
Însă în secvența de mai sus doar am inițializat fereastra grafică, specificând limitele de abscise și ordonate ale punctelor care urmează să fie calculate și plotate ulterior; în loc de abscise și ordonate (așteptate de regulă), am indicat doar "0" — caz în care, chiar și fără a mai specifica type="n", actualmente nu se plotează nimic.
De observat totuși această adecvare la datele existente, a comenzii:

#inițializează fereastra grafică în care se vor plota punctele curbei
plot(range(X), range(Y), type = "n", asp = 1)

În loc să specificăm direct 0, xlim și ylim, am indicat indirect (prin range()) minimul și maximul pentru abscise și ordonate; punctele calculate astfel nu vor fi plotate (fiindcă am setat type="n"), dar orice plotare ulterioară va ține seama de limitările rezultate.

Punctele au fost plotate câte unul, invocând de fiecare dată points() (specificându-le anumite atribute de formă și mărime, culoare, etc.) — rezultând conturul zdrențuit din figura de mai sus; dacă pentru secvențele X și Y am fi folosit un pas mai mic (ca 0.001) atunci erau găsite (de 10 ori) mai multe puncte ale cercului și conturul apărea mai puțin zdrențuit — dar timpul de execuție ar fi crescut sensibil (iar dacă îndrăznim să angajăm un pas și mai mic, 0.0001 — riscăm poate, ca sistemul să "înghețe").
Am dori desigur, un contur neted (nu cu puncte), dar n-am fi putut folosi lines(), fiindcă lines() pretinde nu un punct, ci abscisele și ordonatele mai multor puncte, urmând ca în loc de puncte să ploteze micile segmente care le-ar uni unul cu următorul, creând impresia de "neted" (cu grija că folosind lines(), poate apărea un efect nedorit: apariția unui segment de la ultimul, la primul punct).

Este clar că invocând comenzi de plotare în interiorul ciclurilor, durata execuției crește foarte mult; deci întâi ar trebui înregistrate coordonatele punctelor curbei, într-o anumită structură de date — apoi, pentru trasarea grafică a datelor respective va fi necesară o singură comandă de plotare, fără a o repeta (chiar plot() dacă n-am inițializat încă o fereastră grafică, altfel lines(), sau chiar points() cu type="l").

Nu este necesar să constituim ad-hoc o asemenea structură de date, fiindcă dispunem de funcția outer(); primind vectorii X$=(x_1,x_2,\ldots,x_n)$ și Y$=(y_1,y_2,\ldots,y_n)$, aceasta constituie intern o matrice cu elementele $z_{ij}=(x_i,\,y_j)$ și aplică asupra acesteia funcția "FUN" indicată ca argument — returnând matricea de tip $n\times n$ care pe locul $(i,j)$ conține valoarea FUN$(x_i,\,y_j)$. Desigur, comanda de plotare (de obicei, contour()) va avea nevoie de toți cei trei vectori, X, Y și Z.
De observat însă că astfel, avem toate valorile luate de "FUN" pe domeniul rectangular X×Y (pentru cazul cercului de mai sus am avea de selectat numai valorile zero, de fapt aproximativ egale cu 0). Dar este avantajos să avem toate valorile funcției: ne-ar putea interesa familia de curbe definită de $f(x,y)=\lambda$, unde $\lambda$ să aibă și alte valori decât zero; e de amintit că R a fost destinat din start cercetărilor statistice, în care interesează mai multe niveluri ale unor indicatori statistici; iar în "grafica 3D" interesează curbele rezultate intersectând o suprafață $f(x,y,z)$ cu plane $z=\lambda$ fiindcă în fond, "forma" unui obiect este dată nu de unul, ci de mai multe contururi…

Obs. Cercul considerat mai sus este intersecția suprafeței conice $x^2+y^2=z^2$ cu planul $z=R$ (care este perpendicular pe axa $Oz$ a conului).

Având vectorii (ordonați crescător) X, Y și matricea Z (în forma introdusă de outer()), funcția contour() va plota (și numai atât) curbele de nivelurile Z=$\lambda$ care îi sunt indicate.
contour() nu returnează datele respective — la urma urmei, valorile Z există deja, din apelul anterior al funcției outer()…; totuși, contour() rearanjează intern matricea Z (încât plotarea să decurgă "de sus în jos și de la stânga spre dreapta") și pe de altă parte, procedează mai complicat ("mai fin") decât să ploteze direct punctele $(x,y)$ pentru care Z=$\lambda$ — anume, pentru fiecare punct $(x,y)$ analizează și valori din Z luate în puncte vecine acestuia (căutând cumva o medie potrivită a valorilor funcției pe fiecare "pătrățel" care conține punctul curent — ceea ce amintește iarăși, de caracterul statistic specific lui R).

În schimb, contourLevels() face (probabil) același lucru ca și contour(), dar nu plotează, ci returnează datele calculate — anume, sub forma unei liste care asociază fiecărui nivel dintre cele indicate, câte una sau mai multe (sub) liste conținând coordonatele necesare plotării contururilor de pe nivelul respectiv.

N.B. Am încercat, ne-am străduit noi, să explicăm pe scurt lucrurile (dar nici altundeva, nu găsești cine știe ce "explicații"). Dar dacă te uiți mai bine și analizezi cât de cât, codul-sursă contourLines.h (v. de exemplu r-source, fișierul src/main/contour-common.h)… probabil că explicațiile de mai sus referitoare la "contours" trebuie calificate ca "barbare".

Următoarea funcție, primind în $H$ matricea returnată de contourLines(), plotează curba corespunzătoare (sau curbele, dacă s-au indicat mai multe niveluri) — în mod corect, adică ținând seama de faptul că pentru un același nivel pot exista în $H$ mai multe (sub)contururi:

plot_contours <- function(H, ...) {
    # calculează limitele Ox/Oy ale contururilor de pe fiecare nivel
    lim <- sapply(1:length(H), function(i) 
                  c(range(H[[i]]$x), range(H[[i]]$y)))
    # limitele Ox/Oy pentru nivelul, sau nivelurile respective 
    xlim <- range(lim[, 1])
    ylim <- range(lim[, 2])
    # inițializează fereastra grafică (cu limitele găsite)
    plot.new()
    plot(xlim, ylim, type = "n", asp=1, ...)
    # plotează (separat) fiecare contur de pe nivel (sau niveluri)
    for(j in 1:length(H))
        lines(H[[j]]$x, H[[j]]$y, ...)
}

Contururile de pe un același nivel trebuie plotate separat, fiindcă altfel lines() ar produce de obicei, un segment suplimentar între ele…

Am folosit și anterior contourLevels() (v. asupra ovalelor Cassini), dar "incorect" — având doar noroc de faptul că în contextul respectiv, pe nivelul indicat exista un singur contur. Am înțeles ceea ce am evidențiat mai sus – că "pentru un același nivel pot exista în $H$ mai multe (sub)contururi" — abia mai târziu, în urma unui experiment conjunctural, evocat mai jos.

Să considerăm curbe mai complicate decât un cerc, sau o conică — de exemplu:

FUN <- function(x, y)  # o curbă (de grad 4, "quartic") cu un "tacnode"
    2*x^4 - 3*x^2*y + y^2 - 2*y^3 + y^4
X <- Y <- seq(-1.6, 2.1, by=0.001)
Z <- outer(X, Y, FUN)
H <- contourLines(X, Y, Z, levels = 0)
plot_contours(H, lwd = 1.05)

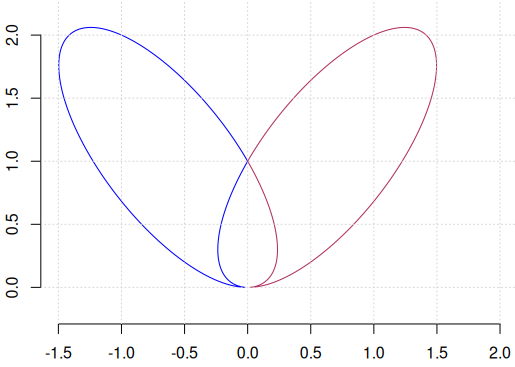
Funcția plot_contours() are un argument "...", prin care parametrul grafic lwd (setat în apelul de mai sus, lwd=1.05) a fost transmis funcției lines() (invocată în final de plot_contours()), pentru a mări puțin grosimea ("line width") liniei de trasare.

Să verificăm structura de date furnizată în H de către contourLines() (cu levels = 0):

> str(H)
List of 2
List of 2  # cu două subliste (ambele, pentru nivelul 0)
 $ :List of 3  # primul contur
  ..$ level: num 0
  ..$ x    : num [1:7541] -1.5 -1.5 -1.5 -1.5 -1.5 ...
  ..$ y    : num [1:7541] 1.72 1.73 1.73 1.73 1.73 ...
 $ :List of 3  # al doilea contur
  ..$ level: num 0
  ..$ x    : num [1:7541] 0.001 0.000333 0.001 0.000334 0.001 ...
  ..$ y    : num [1:7541] 0.998 0.999 1 1.001 1.002 ...

Desigur, nu ne lăsăm păcăliți de valorile redate mai sus (la afișare, de obicei valorile reale sunt "reduse" la două-trei zecimale semnificative):

> H[[1]]$x[1:6]; H[[1]]$y[1:6]  # valori de pe primul contur
[1] -1.496000 -1.496021 -1.496072 -1.496122 -1.496170 -1.496217
[1] 1.724599 1.725000 1.726000 1.727000 1.728000 1.729000

Am intervenit puțin în funcția plot_contours(), pentru a reda primul contur (corespunzător listei H[[1]]) cu "blue", iar pe al doilea cu "maroon". Cele două ramuri au punctul comun (0,1) și se întâlnesc (într-un mod aparte) în punctul (0,0).
Originea aparține curbei (fiindcă FUN(0,0)=0), dar observăm că nu apare plotată pe graficul redat mai sus; aceasta, fiindcă avansând pe $Ox$ și $Oy$ cu pasul considerat 0.001 (cu aproximații inerente), nu se ajunge la (0.0,0.0). Dar curba respectivă este continuă (inclusiv, în (0,0)), iar cele două "ramuri" se ating în origine într-un mod special: au aici nu numai aceeași tangentă, dar și un același cerc osculator (fiindcă primele derivate în zero sunt nule); un asemenea punct al unei curbe se numește "tacnode" (am aflat că astfel de noduri sunt importante pentru proiectarea drumurilor rutiere).

Să testăm acum comportarea funcției noastre plot_contours, în situația când cerem plotarea mai multor niveluri Z; pentru aceasta considerăm o curbă complicată (pentru care nu găsim nicio semnificație și probabil a fost constituită artificial, în scopul ilustrării anumitor algoritmi), a cărei ecuație am preluat-o răsfoind o carte de "Rational Algebraic Curves" (cu subtitlul semnificativ "A Computer Algebra Approach") apărută în 2008 (la Springer), dar și publicată (recent) pe Internet de către autori (J. Rafael Sendra, Franz Winkler și Sonia Pérez-Díaz):

FUN <- function(x, y)
    1+x-15*x^2-29*y^2+30*y^3-25*x*y^2+x^3*y+35*x*y+x^4-6*y^4+6*x^2*y
X <- Y <- seq(-4.5, 6.5, by=0.01)
Z <- outer(X, Y, FUN)
H <- contourLines(X, Y, Z, levels = seq(-9, 9, by = 3))
plot_contours(H, lwd=1.05)

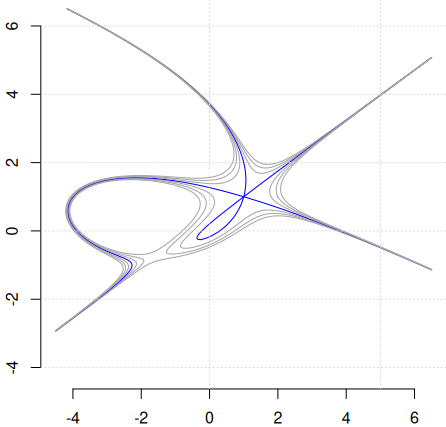
Investigând lista H, am constatat că nivelul zero care ne interesează este reprezentat în H[[8]] și H[[9]] (două contururi) și astfel, intervenind puțin în plot_contours(), am putut să-l evidențiez prin "blue" (iar celelalte 6 nivele ale suprafaței, prin "gray"). Curba respectivă ni s-a părut chiar ciudată: parcă ar fi două curbe independente, cu un punct comun în $(1,\,1)$ (într-o asemenea situație, am plota una și am adăuga-o apoi pe cealaltă); dar în cartea menționată se găsește printr-un anumit algoritm, o parametrizare rațională — însemnând implicit că polinomul respectiv este ireductibil (deci, dacă am înțeles bine, nu poate fi vorba de componente independente).

Pe de altă parte, n-am reușit să plotăm curba folosind (în loc de plot_contours()) parametrizarea indicată în carte — ne-a rezultat un grafic "aiurea"… Am obținut însă graficul corect folosind o altă parametrizare rațională (foarte diferită de cea evocată mai sus), furnizată prin funcția rational_parameterization() din SageMath.
Subliniem că de obicei, o reprezentare parametrizată are forma $x=\pm\;x(t),\,\,y=\pm\,y(t)$, cu $x(t)$ și $y(t)$ funcții (raționale) de parametrul $t$; ca urmare, comenzile de plotare vor trebui să vizeze separat, cele patru cadrane $xOy$ — altfel spus, am avea de vizat, într-o funcție similară ca idee cu plot_contours(), patru "sub-contururi".