Problema orarului școlar echilibrat și limbajul R
[1] SCHAERF, A. A survey of automated timetabling. Artificial intelligence review 13, 2 (1999), 87–127.
[2] V. Bazon - Problema orarului școlar, pe tărâmul limbajului R (Google Play/Books; 50 lei)
Introducere
Problema orarului școlar—School Timetable Problem, STP—constă în a repartiza anumite resurse date (tupluri de profesori,
grupuri de elevi și săli de clasă), pe anumite sloturi de timp (cupluri (Zi, Oră)), astfel încât să se evite suprapunerile și să fie satisfăcute într-o proporție cât mai mare, anumite preferințe inițiale.
STP este tratată de obicei (v. [1]) ca „problemă combinatorială de căutare și optimizare”, concretizând și dezvoltând teorii, tehnici și euristici (simulated annealing, evolutionary algorithms, integer programming, constraint programming, etc.) care vor fi adus (în ultimii vreo 50 de ani) câștiguri importante pentru informatică și programare.
[2] conturează totuși altă direcție pentru STP, observând în mod direct realitatea: încadrarea profesorilor dintr-o școală dată este un „set de date”, care trebuie completat cumva, pentru a deveni un orar (care este un alt set de date).
Setul inițial conține toate lecțiile prof | obj | cls care trebuie desfășurate în săptămâna curentă și avem de adăugat coloana Zi și apoi coloana Ora, astfel încât:
(1) – repartizarea pe zile a lecțiilor să fie echilibrată (pe zile, clase, profesori și obiecte);
(2) – să nu existe suprapuneri de lecții într-o aceeași oră a zilei (exceptând cuplajele);
(3) – pe o zi sau alta, fiecare profesor să aibă cel mult două ferestre.
Iar după obținerea unui astfel de orar, avem de coborât pe cât se poate numărul total de ferestre, pe fiecare zi.
În principiu, montarea variabilei Zi pe tabelul lecțiilor decurge prin generare aleatorie a valorilor acesteia, până când sunt satisfăcute condițiile (1) (fiind foarte multe repartizări posibile, avem suficiente șanse de a nimeri una cât mai potrivită). Cam la fel, adăugăm și câte o coloană Ora, încât să fie îndeplinite condițiile (2) și (3): permutăm aleatoriu lecțiile repartizate în câte o aceeași zi și ținem seama de anumite proprietăți ale unor grafuri asociate acestora. Prevedem și posibilități de retușare interactivă (prin consola R).
Pentru aceste seturi de date folosim consecvent „forma normală”: datele propriu-zise sunt valorile posibile ale câte uneia dintre niște variabile independente fixate (nu amestecăm profesorii și obiectele; nu operăm cu „sloturi”, ci vizăm separat variabilele Zi și Ora); orice investigație dorim, va decurge folosind operații de filtrare (pentru linii de valori) și de selectare (de variabile, sau coloane) – iar pentru facilitare, transformăm o coloană sau alta în factor (ceea ce asigură și operații de grupare și „splitare”).
R împreună cu „dialectul” tidyverse și cu pachetul igraph ne oferă tipurile corelate de date ('data.frame', 'matrix', 'list', 'graph' etc.) și metodele de lucru (filtrare, selectare, adăugare, grupare, etc.) necesare implementării ideii evidențiate mai sus.
Bineînțeles că în mod implicit, [2] ajunge să fie și un soi de „manual”, sau compendiu de folosire a limbajului R și a pachetului tidyverse (într-un context de programare diferit totuși, de orientarea statistică specifică mediului R).
Procurarea datelor inițiale
Programele R de repartizare pe zile și pe orele zilei a lecțiilor, au fost dezvoltate plecând de la seturi de date inițiale deduse de pe orare generate prin aplicația asctimetables, orare postate (în format PDF, HTML sau Excel) pe site-urile unor diverse școli din țară.
Numele de profesori care apar în [2] au fost generate aleatoriu și nu corespund unor persoane reale; declarăm că numele de profesori care apar uneori mai jos, sunt și ele, fictive (ni s-a părut inutil, efortul de a le înlocui din start cu nume generate aleatoriu).
De pe site-ul unei școli am obținut un fișier PDF conținând orarele claselor; redăm aici pagina corespunzătoare uneia dintre clase:
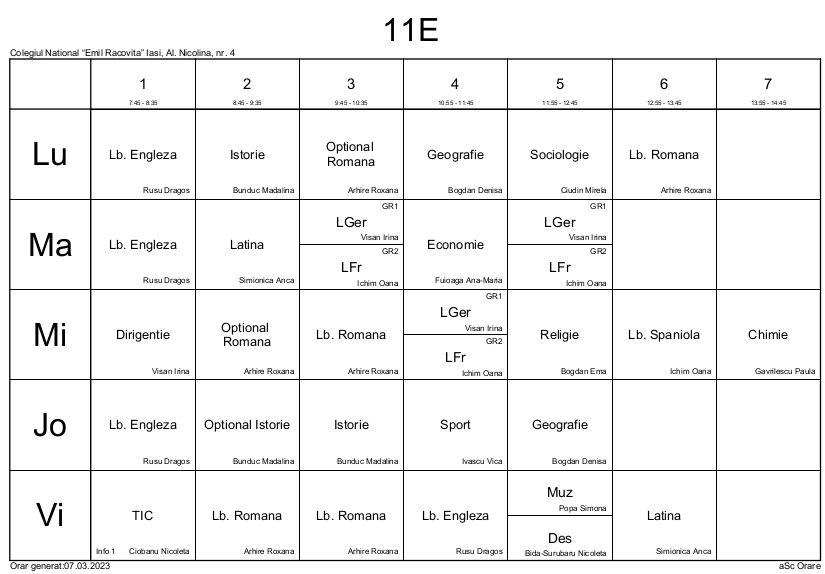
Folosind gs (v. Ghostscript) cu -sDEVICE=txtwrite, obținem orarele claselor într-un format textual care păstrează cu aproximație (spațiind între coloane), formatul original.
Redăm aici (de sub editorul de text mousepad) primele trei coloane din primele linii ale fișierului-text rezultat pentru pagina PDF expusă mai sus:

Este necesară vreo oră de muncă de editare atentă, pentru a aduce fișierele-text respective la un format unitar, evidențiind datele de care avem nevoie:

Anume, am eliminat antetele de pagină (numele și adresa școlii, respectiv "Orar generat... aSc Orare"), precum și linia de intervale orare "7:45 – 8:35 ..."; am comasat nume de obiecte care inițial erau despărțite pe două sau mai multe rânduri (de exemplu, "Optional Romana"). Pentru lecțiile care se desfășoară „pe grupe”, am eliminat "GR1" și "GR2" și am „unificat” numele celor doi profesori, alipindu-le printr-un caracter "/" (la fel, pentru numele celor două obiecte implicate în cuplajul respectiv).
În urma acestei editări, fișierele-text respective conțin câte 12 linii de date (și eventual, o linie vidă la sfârșit); prima linie conține doar numele clasei; pe a doua linie avem orele 1..6 sau 1..7; pe liniile 3 și 4 avem orarul clasei pe ziua Lu (obiectele pe linia 3 și profesorii corespunzători pe linia 4); pe liniile 5 și 6 – orarul pe ziua Ma, ș.a.m.d.
Fiecăruia dintre fișierele-text obținute îi asociem prin readLines() un vector conținând (ca șiruri de caractere) cele 12 linii din fișier; de exemplu:
> Lines[3] [1] " Lu Lb. Romana Geografie Informatica si TIC Matematica"
Eliminăm spațiile inițiale și finale și apoi ținem seama de faptul că datele din coloane vecine sunt separate între ele printr-o secvență de cel puțin două spații; prin stringr::str_split() transformăm șirurile de caractere în vectori, cu câte un număr de componente egal cu numărul de ore din ziua respectivă (eventual plus 1, pentru numele zilei):
> Q[[3]] [1] "Lu" "Lb. Romana" "Geografie" "Informatica si TIC" "Matematica"
Se poate ca numărul de ore să difere de la o zi la alta; în acest caz, completăm vectorul respectiv cu valori NA (pentru a aplica list2DF(), vectorii trebuie să aibă aceeași dimensiune).
Apoi, prin map_dfr și list2DF transformăm listele de vectori într-un „tabel” data.frame, conținând toate datele orarului pe coloanele prof, obj, zi, ora și cls:
library(tidyverse) path <- "EM_cls/" # Subdirectorul fişierelor (editate) "cls-*.txt" txt2DF <- function(cls_txt) { con <- file(paste0(path, cls_txt)) Lines <- readLines(con, warn=FALSE) # Vector cu cele 12/13 linii din 'cls-*.txt' close(con) Lines <- Lines[1:12] # linia 13, dacă există este vidă Q <- Lines %>% str_trim(., side="both") %>% str_split(., "\\s{2,}") no <- length(Q[[2]]) # numărul maxim de ore pe zi, ale clasei for(i in 3:12) { Li <- Q[[i]] n <- if(i %% 2) no+1 else no # liniile impare încep cu numele zilei if(length(Li) == n) next while(length(Li) < n) Li <- c(Li, NA) # completează când este cazul, cu valori NA Q[[i]] <- Li } map_dfr(seq(3, 11, by=2), function(i) list2DF(list( prof = Q[[i+1]], obj = Q[[i]][-1], zi = rep(Q[[i]][1], no), ora = 1:no)) ) %>% mutate(cls = Q[[1]]) } EM <- map_dfr(list.files(path=path, pattern=".txt"), txt2DF) # 1115 obs. EM <- EM %>% filter(!is.na(prof)) #'data.frame': 1018 obs. of 5 variables: saveRDS(EM, file="EMorig.RDS")
După eliminarea în final, a liniilor cu valori NA, ne-au rămas 1018 lecții prof|obj|zi|ora|cls și le-am salvat în fișierul EMorig.RDS. Pentru programele din [2], de repartizare echilibrată a lecțiilor pe zile și pe orele zilei, ne interesează numai datele de încadrare prof|obj|cls.
Simplificări, codificări și asocieri prealabile
Folosind editorul de text gedit, constituim un program prin care investigăm datele (cel mai adesea, interactiv – din consola R), urmând să le adaptăm treptat specificațiilor din [2]:
# sicoas.R library(tidyverse) EM <- readRDS("EMorig.RDS") > str(EM) # inspectăm interactiv structura datelor 'data.frame': 1018 obs. of 5 variables: $ prof: chr "Istudor Ramona" "Fosalau Manuel" ... $ obj : chr "Lb. Romana" "Geografie" "Informatica si TIC" "Matematica" ... $ zi : chr "Lu" "Lu" "Lu" "Lu" ... $ ora : int 1 2 3 4 1 2 3 4 5 6 ... $ cls : chr "05A" "05A" "05A" "05A" ...
Să vedem și câteva eșantioane aleatorii de linii (repetând slice_sample()):
> slice_sample(EM, n=3) prof obj zi ora cls 1 Ivascu Vica Sport Ma 6 10E 2 Frost Alina/Nenov Simona LGer/LFr Lu 3 09A 3 Popa Simona Muzica Ma 1 08C
Deși nu este neapărat necesar, vom simplifica—și corecta, eventual—denumirile obiectelor (înlocuind "Lb. Romana" cu "Română", etc.), precum și numele claselor (preferând "9A" în loc de "09A"). Vom încerca să codificăm profesorii după disciplinele principale și numărul de ore ale fiecăruia; pentru încadrările „pe grupe” (cum vedem mai sus pe obiectul "LGer/LFr") vom introduce „profesori fictivi” și vom asocia anumite dicționare de legături.
În final, vom elimina coloanele zi și ora (iar câmpul obj va fi necesar numai când va fi de afișat orarul pe care-l vom obține prin programele din [2]).
Să „corectăm” întâi numele claselor:
EM <- EM %>% mutate(cls = sub("^0", "", cls)) # elimină prefixul "0" (09A -> 9A)
Pentru a modifica numele obiectelor (pe toate liniile), întâi transformăm în factor coloana respectivă:
EM <- EM %>% mutate(obj = factor(obj, ordered=TRUE))
levels(EM$obj) ne afișează în consolă disciplinele respective, indexând liniile sub forma "[1]" – adică alipind '[', o secvență de cifre și ']', corespunzător expresiei regulate \[\d*\]; copiem liniile în gedit și întâi eliminăm indecșii de linie, folosindu-ne de meniul Find and Replace (care are și opțiunea de căutare după expresii regulate); prin același meniu, putem apoi înlocui spațiile dintre denumiri (redate fiecare, între ghilimele) cu o virgulă – obținând după ambalarea în c(...
Modificăm (în gedit) elementele acestui vector și apoi îl copiem în program într-o variabilă OBJ. Vom avea de folosit denumirile din OBJ numai când va fi să afișăm orare, nu și în programele de generare a orarelor; dar în loc să le eliminăm pur și simplu, le abreviem la câte două caractere și le folosim astfel pentru a codifica profesorii: de exemplu, codul "Bi3" ar reprezenta un profesor de "Biologie" – anume pe al treilea încadrat pe acest obiect, în ordinea descrescătoare a numărului de ore.
Abreviem deci numele obiectelor și transformăm OBJ într-un „dicționar” (prin funcția names()) care precizează asocierea dintre abrevieri și denumiri:
> OBJ # dicționarul disciplinelor AB Bi Ch CP De "AB" "Biologie" "Chimie" "CoProgramare" "Desen" Di Ec EA ES FL "Dirigenție" "Economie" "EdAntrep" "EdSocială" "Filosofie" Fi Ge IA IP IC "Fizică" "Geografie" "InfApl" "InfoAplicații" "InfoCurs" IT IRC IRO Is Ju "InfoTIC" "IR/OpCh" "IR/OS" "Istorie" "Jurnalism" La En Fr Ge Ro "Latină" "Engleză" "Franceză" "Germană" "Română" Sp GF Li Lo Ma "Spaniolă" "Ger/Fra" "LitUniv" "Logică" "Matematică" MUD Mu OIB OCB OB "Muz/Des" "Muzică" "OI/OpBi" "OpCh/OpBi" "OptBiologie" OC OI OM OR OS "OptChimie" "OptIstorie" "OptMatematică" "OptRomână" "OptSport" Ps Re So Sp Te TI "Psihologie" "Religie" "Sociologie" "Sport" "Tehnologie" "TIC"
Salvăm dicționarul disciplinelor și înlocuim prin abrevieri, denumirile din EM$obj:
saveRDS(OBJ, "dctObj.RDS") levels(EM$obj) <- names(OBJ)
Când va fi să afișăm orare, vom încărca dctObj.RDS și vom ști atunci, că lecțiile profesorului "Ro4" de exemplu, trebuie afișate ca "Română".
De observat funcționalitatea bilaterală a funcției levels(): furnizează nivelele factorului, dar permite și modificarea ulterioară a nivelelor (de altfel și alte funcții, de exemplu names(), asigură atât operații "Get" cât și operații "Set").
Codificarea profesorilor și cuplajelor
Să despărțim lecțiile obișnuite („cu întreaga clasă”), de cele care decurg „pe grupe” (pentru care în câmpul prof apare ’/’) și să evidențiem profesorii în fiecare caz:
L12 <- EM %>% split(grepl("/", .$prof)) P1 <- L12[[1]] %>% pull(prof) %>% unique() %>% sort() # cei care au și ore proprii ("cu clasa întreagă") P2 <- L12[[2]] %>% pull(prof) %>% unique() %>% strsplit(., "/") %>% unlist() %>% unique() %>% sort() # profesorii angajați în cuplaje ("pe grupe") print(setdiff(P2, P1)) # character(0) (Nu există profesori "externi")
Constatăm prin setdiff() că nu există profesori „externi” (care nu au ore proprii, ci doar în cuplaje); aceasta simplifică lucrurile, față de cazurile tratate în [2].
Următoarea funcție produce disciplinele pe care este încadrat un profesor (din setul P1, sau din P2), în ordinea descrescătoare a numărului de ore:
prof_objs <- function(P, lss) lss %>% filter(grepl(P, prof)) %>% count(obj, sort=TRUE)
Subliniem că prof_objs() păstrează calitatea de factor a câmpului $obj și implicit, toate nivelele acestuia; dacă un profesor este încadrat pe mai multe discipline, ne va interesa acum numai cea „principală” (pe care are cel mai multe ore) și va trebui să folosim droplevels(), pentru a păstra numai nivelele corespunzătoare disciplinelor principale.
Putem obține acum o listă care asociază fiecărei discipline principale, setul profesorilor încadrați pe acea disciplină, ordonați descrescător după numărul de ore:
Pob <- map_dfr(P1, function(P) { OB <- prof_objs(P, L12[[1]])[1, ] if(P %in% P2) { # decide asupra disciplinei principale OB2 <- prof_objs(P, L12[[2]])[1, ] if(OB2$n > OB$n) OB <- OB2 } data.frame(prof = P, obj = OB$obj, no = OB$n) }) %>% droplevels() %>% # ignoră disciplinele secundare arrange(desc(no)) %>% split(.$obj)
În sfârșit – putem formula un „tabel” care asociază numelor din P1 coduri de câte 3 caractere, formate din codul disciplinei principale și un sufix care indică numărul de ordine după numărul descrescător al orelor fiecăruia:
Pcd <- map_dfr(seq_along(Pob), function(i) { N <- nrow(Pob[[i]]) # numărul de profesori pe disciplina curentă (< 10) ob <- Pob[[i]]$obj[1] obn <- paste0(ob, 1:N) data.frame(prof = Pob[[i]]$prof, cod = obn) })
Dar bineînțeles că în loc de „tabel”, va fi mai convenabil să lucrăm cu dicționare:
prof_cod <- Pcd$cod names(prof_cod) <- Pcd$prof CPR <- setNames(names(prof_cod), prof_cod) # dicționar nume_profesor -> COD
Folosind dicționarul prof_cod, putem codifica acum și cuplajele – alipind
codurile celor doi membri (iar în final, reunim toate codurile):
tws <- L12[[2]] %>% pull(prof) %>% unique() %>% sort() # cuplajele de profesori, de forma Prof1/Prof2 cup_cod <- vector("character", length(tws)) for(i in seq_along(tws)) { tw <- strsplit(tws[i], "/")[[1]] # legasem prin "/" cele două nume dintr-un cuplaj kod <- as.vector(prof_cod[tw]) # codurile membrilor cup_cod[i] <- paste0(kod[1], kod[2]) # alipește codurile membrilor } cup_cod <- setNames(cup_cod, tws) prof_cod <- c(prof_cod, cup_cod) # dicționar profesor sau cuplaj -> COD saveRDS(prof_cod, "dctProf.RDS") # util când va fi de afișat orarul final
Dicționarul prof_cod va fi util—dacă-l vom inversa— când va fi să afișăm orarul final.
Înregistrăm codurile din vectorul prof_cod, pe toate liniile din setul EM:
EM <- EM %>% mutate(prof = as.vector(prof_cod[prof]))
Să observăm pe un eșantion, că unii profesori au și discipline secundare:
> slice_sample(EM, n=5) prof obj zi ora cls 1 TI2 IP Mi 2 11B # "IP" este disciplină secundară a lui "TI2" 2 TI2 TI Ma 1 9C # "TI" este disciplina principală a lui "TI2" 3 Ma2 Ma Mi 5 6A 4 De1 De Lu 7 8C 5 GF2GF3 GF Lu 4 12D
Fiecare lecție este reprezentată pe câte o linie din setul EM; pe linia respectivă, codul din câmpul prof induce pe cel din câmpul obj numai în cazul disciplinelor „principale” – deci comparând pe fiecare linie, valorile prof și obj, vom putea depista liniile corespunzătoare disciplinelor secundare.
În mod implicit, operațiile pe un obiect data.frame decurg „pe coloane”; dar funcția dplyr::rowwise() asigură și posibilitatea de a opera „pe linii”, cum am avea nevoie acum:
scd <- EM %>% rowwise() %>% filter(! grepl(obj, prof)) # liniile cu discipline "secundare" lSC <- scd %>% split(.$prof) OSE <- map_dfr(seq_along(lSC), function(i) { sec <- lSC[[i]] # pe profesorul curent map_dfr(seq_along(unique(sec$obj)), function(j) { Obj <- sec$obj[j] # pe fiecare disciplină secundară Cls <- sec %>% filter(obj == Obj) %>% pull(cls) data.frame( prof = sec$prof[1], obj = Obj, cls = paste(Cls, collapse = " ")) }) })
Pentru a ne convinge că lucrurile sunt în regulă, să listăm liniile din OSE și frecvența pe discipline a lecțiilor din EM, corespunzătoare unuia dintre profesori:
> OSE %>% filter(prof == "TI1") prof obj cls 1 TI1 Di 9B 2 TI1 IP 9B 10D 12B 12B 12B 12B 3 TI1 IC 9D > ti1 <- EM %>% filter(prof == "TI1") > frq <- table(ti1$obj); print(frq[frq != 0]) Di IP IC TI 1 6 1 11
Pe exemplul redat aici, vedem că profesorul "TI1" are disciplina principală (pe 11 ore) "TI" (abrevierea adoptată pentru TIC) și are mai multe discipline secundare: o oră "Di" (Dirigenție) la clasa 9B, 6 ore "IP" (InfoAplicații) și o oră "IC" (InfoCurs) la clasa 9D.
De notat că aici am făcut un mic pas înainte față de [2], unde consideram doar cazul (cel mai obișnuit) când un profesor are cel mult o singură disciplină secundară (caz în care era suficient un singur map_dfr(), nu două imbricate, ca mai sus).
Când va fi de afișat orarul vreunei clase, va trebui să consultăm și OSE:
saveRDS(OSE, "dfObjSec.RDS")
pentru a stabili ce disciplină afișăm pe lecția curentă a unuia sau altuia dintre profesori.
Dicționarele dependențelor
Alocarea pe zile și ore a lecțiilor cuplajelor și profesorilor care sunt angajați în cuplaje, va depinde mereu de alocările făcute celor cu care sunt astfel conexați; vom constitui niște „dicționare” care să evidențieze aceste dependențe.
Împărțim lecțiile în două părți, după lungimea codului (3 sau 6) din $prof și degajăm profesorii din fiecare parte:
S36 <- EM %>% split(nchar(.$prof)) K3 <- S36[[1]] %>% pull(prof) %>% unique() %>% sort() K6 <- S36[[2]] %>% pull(prof) %>% unique() %>% sort()
Următorul dicționar are drept chei profesorii care intră măcar într-un cuplaj și care au și ore proprii, iar drept valori – vectorii care conțin profesorii de care depind aceștia, la alocarea pe zile și ore:
Tw1 <- map(K3, function(P) K6[grepl(P, K6)]) %>% setNames(K3) %>% compact()
Dacă P este una dintre cheile lui Tw1, ora din zi pe care o vom aloca uneia dintre lecțiile lui P trebuie să nu coincidă cu vreuna dintre orele alocate deja cuplajelor din vectorul Tw1[[P]]:
P Tw1[[P]] $Bi1 "Bi1Fi1" "Ch3Bi1" "IP1Bi1" $Ch1 "Re1Ch1" $Ch3 "Ch3Bi1" $De1 "Mu1De1" $ES1 "La1ES1" $Fi1 "Bi1Fi1" $Fr1 "GF1Fr1" "GF2Fr1" $GF1 "GF1Fr1" "GF1GF3" "GF1GF4" $GF2 "GF2Fr1" "GF2GF3" "GF2GF4" $GF3 "GF1GF3" "GF2GF3" $GF4 "GF1GF4" "GF2GF4" $IP1 "IP1Bi1" $La1 "La1ES1" $Mu1 "Mu1De1" $Re1 "Re1Ch1"
Constituim (mai simplu ca în [2], fiindcă acum nu avem profesori „externi”) și un dicționar cumva invers, în care cheile sunt cuplajele existente, iar valorile sunt vectori care conțin profesorii—fictivi sau propriu-ziși—de care depinde alocarea orelor cheii respective:
Tw2 <- map(K6, function(PP) { P1 <- substr(PP, 1, 3) P2 <- substr(PP, 4, 6) setdiff(c(P1, P2, union(Tw1[[P1]], Tw1[[P2]])), PP) %>% unique() }) %>% setNames(K6) %>% compact()
La alocarea lecțiilor unui cuplaj P (cheie din Tw2), va trebui să ținem seama de alocările făcute deja profesorilor și cuplajelor din vectorul Tw2[[P]]:
P Tw2[[P]] $Bi1Fi1 "Bi1" "Fi1" "Ch3Bi1" "IP1Bi1" $Ch3Bi1 "Ch3" "Bi1" "Bi1Fi1" "IP1Bi1" $GF1Fr1 "GF1" "Fr1" "GF1GF3" "GF1GF4" "GF2Fr1" $GF1GF3 "GF1" "GF3" "GF1Fr1" "GF1GF4" "GF2GF3" $GF1GF4 "GF1" "GF4" "GF1Fr1" "GF1GF3" "GF2GF4" $GF2Fr1 "GF2" "Fr1" "GF2GF3" "GF2GF4" "GF1Fr1" $GF2GF3 "GF2" "GF3" "GF2Fr1" "GF2GF4" "GF1GF3" $GF2GF4 "GF2" "GF4" "GF2Fr1" "GF2GF3" "GF1GF4" $IP1Bi1 "IP1" "Bi1" "Bi1Fi1" "Ch3Bi1" $La1ES1 "La1" "ES1" $Mu1De1 "Mu1" "De1" $Re1Ch1 "Re1" "Ch1"
De exemplu, GF1Fr1 nu se va putea afla într-o aceeași oră a zilei ca și vreunul dintre cei 5 profesori (fictivi sau nu) înregistrați în Tw2$"GF1Fr1".
Repartizarea pe zile și pe orele zilei a lecțiilor, precum și reducerea ferestrelor din orarele obținute, se bazează pe dicționarele de dependențe; le salvăm împreună:
save(Tw1, Tw2, file="dctTw12.Rda")
Trebuie să verificăm dacă nu cumva, există și clase care depind una de alta (clase cuplate); condiţia ca un cuplaj de profesori să lucreze nu pe câte o grupă a clasei, ci pe clase întregi, rezultate prin combinarea ad_hoc a grupelor a două clase – este apariţia de două ori într-o aceeaşi zi şi oră, a acelui cuplaj:
> EM %>% filter(nchar(prof) > 3) %>% group_by(prof, zi, ora) %>% count() %>% filter(n > 1) # reţinem numai apariţiile duble, dacă există
În cazul de față nu avem clase cuplate (de observat că doar consultând orarul PDF original, nu prea aveam cum să ne dăm seama dacă există sau nu, clase cuplate).
Putem încă folosi variabilele originale Zi și Ora, dacă vrem să investigăm unele caracteristici ale orarului respectiv (distribuția orelor pe zile, pe clase, pe profesor; statistici privitoare la ferestre, etc.). Atfel, nu mai avem nevoie de aceste coloane:
LSS <- EM %>% select(prof, cls) saveRDS(LSS, "lessons.RDS")
Acum în lessons.RDS avem toate lecțiile prof|cls care trebuie desfășurate săptămânal în școala respectivă (am exclus și câmpul obj, devenit inutil în urma codificării pe discipline a profesorilor și a constituirii dicționarului dctObj.RDS și a tabelului dfObjSec.RDS).
Repartizarea echilibrată a lecțiilor, pe zilele săptămânii
Existența unui orar decurge din faptul că încadrarea este normată: pe săptămână, clasele au câte 25-33 ore, profesorii au câte cel mult 18-27 ore, disciplinele au cel mult 7 ore (iar valorile extreme sunt foarte rare); sunt posibile foarte multe orare corecte, astfel că dacă știm să generăm unul oarecare, atunci sunt mari șanse de a nimeri și un orar acceptabil.
Programul by_days.R din [2] definește (pe mai puțin de 70 de linii) o funcție pentru alocarea echilibrată pe zile a lecțiilor profesorilor neangajați în cuplaje și o funcție pentru alocarea (echilibrată) pe zile a lecțiilor celor angajați în cuplaje – de folosit cam așa:
# EMbyDays.R library(tidyverse) LSS <- readRDS("lessons.RDS") Zile <- c("Lu", "Ma", "Mi", "Jo", "Vi") perm_zile <- readRDS("lstPerm47.RDS")[[2]] # cele 120 permutări de 1..5 load("dctTw12.Rda") # [1] listele de dependență "Tw1", "Tw2" source("by_days.R") # funcțiile mount_days_necup() și mount_days_cup() LS1 <- LSS %>% filter(! prof %in% union(names(Tw1), names(Tw2))) # neangajați LS2 <- anti_join(LSS, LS1, by=c('prof', 'cls')) # angajați în cuplaje R1 <- mount_days_necup(LS1) # alocare pe zile a lecțiilor neangajate în cuplaje R2 <- mount_days_cup(LS2) # alocare pe zile a lecțiilor celor angajați în cuplaje R12 <- R1 %>% rbind(R2) # alocarea pe zile a tuturor lecțiilor săptămânii saveRDS(R12, "R12.RDS")
În cazul de față (cu numai 34 de clase, 48 de profesori neangajați în cuplaje și 27 de profesori sau „profesori fictivi”, angajați în cuplaje) execuția programului redat mai sus ia cam la fiecare repetare a lui, mai puțin de 10 secunde; însă nu așa („am obținut rezultatul, îl afișăm și gata”) trebuie procedat…
Rezultatele R1 și R2 variază de la o execuție la alta, fiindcă funcțiile de alocare menționate mizează pe aspecte aleatorii (de exemplu, permutări aleatorii de Zile); trebuie repetată execuția programului (de vreo trei ori, în acest caz), până obținem repartiții promițătoare:
> addmargins(table(R1[c('cls','zl')])) zl cls Lu Ma Mi Jo Vi Sum 10A 5 4 4 4 5 22 10B 4 4 4 4 5 21 # ... 9D 4 5 5 4 5 23 9E 5 4 5 5 4 23 Sum 152 152 154 152 153 763 # distribuție aproape uniformă > addmargins(table(R2[c('cls','zl')])) zl cls Lu Ma Mi Jo Vi Sum 10A 1 3 1 2 1 8 10B 3 2 2 3 0 10 10C 1 2 2 1 2 8 # ... 9D 0 2 2 2 2 8 9E 2 1 0 2 2 7 Sum 50 50 52 52 51 255 # distribuție aproape uniformă
În R1 (nu neapărat și în R2) obținem totdeauna distribuții omogene pentru orele claselor (diferența pe clasă între o zi și alta este de cel mult o oră), însă trebuie să repetăm eventual execuția programului, pentru a obține o distribuție cât mai apropiată de uniform, a totalului de ore pe zi (precum mai sus, 152 152 154 152 153). Doar având R1 și R2 suficient de omogene, putem anticipa că și pe profesori, să rezulte câte o distribuție echilibrată a orelor…
Reunind R1 și R2 (în R12), pot apărea excepții: una-două clase cu 8 ore într-o zi și 4 în altele; sau, unii profesori—dintre cei angajați în cuplaje—cumulează distribuții dezechilibrate pe zile. Folosind funcțiile de ajustare interactivă (de la consola R) prezentate în [2], putem transforma cu ușurință R12, astfel încât distribuția lecțiilor să fie omogenă pe zile (anume, 204 203 203 204 203) și pe clase și cu câteva excepții, să fie omogenă și pe profesori (pentru majoritatea distribuțiilor individuale, diferența de ore între zile este de cel mult o oră).
În plus, putem folosi o aplicație interactivă javaScript + HTML precum recast/ (v. codul-sursă pe github) – cu avantajul că vedem și putem controla împreună toate datele și pe de altă parte, interschimbăm mai comod clase, dintr-o zi în alta (și cu dezavantajul că avem de transformat între seturile normalizate de date din R și formatul CSV necesar tabelării HTML).
Alocarea lecțiilor dintr-o aceeași zi, pe orele zilei
După ce vom fi definitivat repartizarea pe zile R12, constituim o listă care asociază fiecărei zile, lecțiile prof|cls ale acelei zile:
R12 <- readRDS("R12rec.RDS") # repartizare echilibrată prof|cls|zl ldz <- map(Zile, function(z) R12 %>% filter(zl == z) %>% select(prof, cls) ) %>% setNames(Zile) # lista distribuțiilor prof|cls pe fiecare zi saveRDS(ldz, "R12_ldz.RDS")
Funcția mount_hours() din [2] (pe mai puțin de 80 de linii) etichetează lecțiile unei aceleiași zile cu orele 1..7 ale zilei, astfel încât să se evite suprapunerea a două lecții într-o aceeași oră, să se respecte programul normal (care începe de la prima oră a zilei, pentru toate clasele) și să se creeze cumva premise pentru existența unui număr cât mai mic de ferestre (impunând condiția ca orarele individuale să nu conțină mai mult de două ferestre).
Controlul suprapunerilor necesită informațiile de dependență din dctTw12.Rda – dar acestea trebuie actualizate pe fiecare zi; ca în [2], constituim lPrTz.Rda, conținând listele lTz1 și lTz2 care indică pe fiecare zi, dependențele între profesorii angajați în cuplaje pe acea zi (precum și lista lPrz a tuturor celor care au lecții în ziua respectivă).
Obs. Plecând de la lista map(lTz1, length), putem verifica interactiv în ce măsură lecțiile cuplate sunt repartizate echilibrat pe zile – și eventual, putem decide să mutăm în alte zile unele cuplaje (urmând apoi să reluăm cele de mai sus). Dar subliniem că orice modificare am face acum sau mai departe, asupra repartiției pe zile R12, ea trebuie urmată de actualizarea listei lPrTz.Rda (și deasemenea, de recalcularea coeficienților "betweenness").
mount_hours() alocă lecțiile fiecărei clase în parte, pe orele 1..7 ale zilei; experimentele evocate în [2] privitoare la ordinea lecțiilor respective, au condus la poziționarea fiecărui profesor în raport cu ceilalți în funcție de prezența unor clase comune și la o ordonare aleatorie ponderată de numărul de profesori comuni, a claselor.
Ca în [2], constituim graful profesorilor și graful claselor, în care adiacența reflectă existența unor clase comune, respectiv a unor profesori comuni; reținem în BTW.rda coeficienții "betweenness" ai nodurilor celor două grafuri. Redăm graful claselor pentru ziua Lu (mărimea nodurilor este proporțională cu valorile "betweenness"):
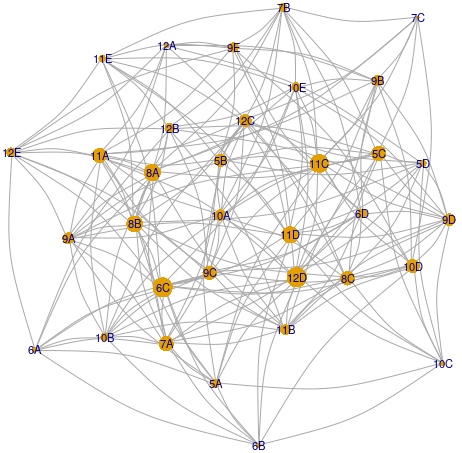
Fixarea orarului unuia dintre cei care au coeficient ”betweenness” mare, ar diminua posibilitățile de alocare ulterioară pentru mult mai mulți profesori (cei aflați pe câte o aceeași geodezică a grafului, cu cel căruia i se fixează orarul), decât fixarea orarului unuia de coeficient ”betweenness” mult mai mic. De aceea, am vizat profesorii și clasele în ordinea crescătoare a coeficienților ”betweenness” (sau una apropiată cumva, de aceasta).
De exemplu, după graful pe Lu redat mai sus, am începe repartizarea pe ore cu lecțiile claselor 7C, 6A, 6C, 10C și am lăsa mai la urmă, pe cele ale claselor mai dense în privința legăturilor comune, 8A, 6C, 11C, 12D; procedând astfel, mărim șansele de reușită pentru alocarea lecțiilor clasei curente (altfel se poate ajunge repede la blocare: oricum am permuta pe ore lecțiile clasei curente, dăm peste lecții cu același profesor, alocate anterior altor clase).
mount_hours() produce foarte repede orarele zilelor, dacă păstrăm plafonul implicit pentru numărul de „ferestre” – 20% din totalul lecțiilor pe ziua respectivă; reducând în cazul de față la 16%, avem totuși timpi buni (sub 5 minute, în total):
06:09:18 30 Lu 06:09:46 # cu 30 de ferestre, "pe orizontale" individuale 31 Ma 06:10:21 30 Mi 06:12:07 33 Jo 06:14:09 29 Vi 06:14:10 > saveRDS(ORR, file="orar1.RDS")
Dar precizăm că s-au avut în vedere numai ferestrele „pe orizontală”, pentru fiecare profesor sau profesor-fictiv în parte… Listăm de exemplu orarele unora dintre lecțiile pe limbi străine, pentru ziua Lu:
> lu <- orarByProf(ORR[["Lu"]]) > lu %>% filter(grepl("GF", prof)) prof 1 2 3 4 5 6 7 1 GF4 - - - 10E - - - 2 GF3 6A 8A - - - - - 3 GF2Fr1 - - - 10C - - - 4 GF1GF4 12A - - - - - - 5 GF2 5D 6D - - - - - 6 GF2GF3 - - - - - 10E - 7 GF2GF4 - - 11E - 12E - - 8 GF1GF3 - - 9C 10A - - - 9 GF1 - - - - 7C 5C -
GF4 intră în ora 1 împreună cu GF1 la clasa 12A, apoi intră împreună cu GF2, în ora 3 la 11E și în ora 5 la 12E, iar ora a 4-a o face singur la clasa 10E; prin urmare, GF4 are o fereastră ascunsă în ora a 2-a – neluată în seamă de mount_hours(), care în schimb consideră că GF2GF4 are o fereastră în ora a 4-a (falsă de fapt, atât pentru GF4 cât și pentru GF2).
Reducerea numărului de ferestre
Încă în mount_hours()—pentru a supraveghea pe parcurs alocarea pe ore a lecțiilor—am folosit un vector de „octeți de alocare”, având drept chei numele profesorilor și drept valori, câte un un octet (de fapt nu chiar 8 biți, ci 32 sau 64 de biți – cât măsoară tipul integer) în care biții erau setați odată cu alocarea de ore, profesorului respectiv: bitul de rang 0..6 corespunde orei 1..7 a zilei.
Șablonând astfel orarele individuale, putem calcula corect și numărul de ferestre; de exemplu, în orarul pe Lu din care am redat mai sus, pentru GF4 avem șablonul binar 0001000, pentru GF1GF4 avem 0000001, iar pentru GF2GF4, 0010100 – care prin „reunire” dau 0011101 (pentru lecțiile în care este implicat GF4); fiindcă avem un singur bit '0' între biți '1', deducem că GF4 are o fereastră (în a doua oră a zilei).
Constituim întâi lista SBC.Rda, conținând drept chei toate șabloanelor binare posibile, de orare individuale cu ferestre (avem exact 99 de asemenea orare, pentru 7 ore; v. problema L445 din Recreații matematice); pe fiecare dintre aceste chei, SBC asociază o listă de „mutări corectoare” – după acest model:
SBC[["5"]] <- list(h1 = c(1,1,3), h2 = c(2,4,2)) # "5" este octetul '00000101'
cu semnificația următoare: fereastra din ora a 2-a a unui profesor care are prima și a treia oră se poate „repara” fie mutându-i clasa din ora h1[1] (=1) în ora h2[1] (=2), fie mutând clasa din ora h1[2] (=1) în ora h2[2] (=4), fie mutând clasa h1[3] (=3) în ora h2[3] (=2). După mutare, profesorul va avea fie primele două ore, fie a 2-a și a 3-a, fie a 3-a și a 4-a oră (fără fereastră).
Desigur, mutând o clasă dintr-o coloană orară în alta, dăm eventual peste lecția la clasa respectivă a unui alt profesor…; pentru a evita suprapunerile, trebuie făcute succesiv mai multe interschimbări de clase, între cele două coloane. În [2] am stabilit că interschimbările necesare sunt date de lanțurile Kempe din graful asociat celor două coloane (conținând ca noduri clasele respective, adiacente dacă aparțin aceluiași profesor) și am formulat o funcție move_cls() care urmărind un asemenea lanț, produce schimbările necesare pe orarul zilei (conform celor două coloane și clasei care i-au fost specificate).
În programul reduce_gaps.R din [2] se identifică ferestrele din orarul zilei curente și folosind SBC, se constituie o „listă de mutări corectoare” pentru aceste ferestre; prin move_cls() se efectuează câte o mutare din lista mutărilor corectoare și în principiu, se înlocuiește orarul inițial cu cel rezultat după mutare, dacă acesta are mai puține ferestre.
Iterând și repetând aceste operații se poate ajunge la o listă de orare zilnice pe care numărul de ferestre este cel mult 5% din totalul lecțiilor pe ziua respectivă. De exemplu, pentru cazul orarului de față (pentru care din mount_hours() rămăsesem cu 29-33 de ferestre pe zi), ne-au rezultat orare zilnice cu 7, 11, 10, 7 și respectiv 6 ferestre (în total, 41 de ferestre; de observat că pe orarul original de la care am plecat existau în total 55 de ferestre); este drept că timpul total de execuție a programului respectiv a fost de aproape 2 ore (pare satisfăcător, dar pe reduce_gaps.R sunt posibile anumite îmbunătățiri semnificative).
Redăm aici orarul pe ziua Lu (cu 204 lecții); coloana suplimentară SB indică șablonul orelor la profesorii propriu-ziși care au ore proprii și sunt angajați și în cuplaje (am adăugat și o coloană pe care am înregistrat disciplinele principale asociate profesorilor):
prof 1 2 3 4 5 6 7 SB Obiect
1 Is3 5A - - - - - - Istorie
2 En6 7C - - - - - - Engleză
3 Ch3Bi1 - 12D - - - - - Chimie (/Biologie)
4 Mu1De1 - - 10B - - - - Muzică (/Desen)
5 TI2 11B 9C - - - - - TIC
6 La1 11E 9E - - - - - Latină
7 Ge3 12B 9D - - - - - Geografie
8 GF4 10E - - - - - - ***-*-- Ger/Fra (Franceză)
9 Bi4 - - - - 12C 11D - Biologie
10 Fi5 12A 9B - - - - - Fizică
11 Fr1 - - - - 7A 6B - ---***- Franceză
12 De1 8B 8C - - - - - ***---- Desen
13 GF3 6A 8A - - - - - **-***- Ger/Fra (Franceză)
14 EA1 10C 10D - - - - - EdAntrep
15 IT1 - - - 7A 8A 6A - InfoTIC
16 GF2Fr1 - - - 10C - - - Ger/Fra
17 Fi2 8C 6D 11B - - - - Fizică
18 Fi4 - - - - 7B 7C - Fizică
19 GF1GF4 - 12A - - - - - Ger/Fra
20 Re2 5D 10C 12D - - - - Religie
21 ES1 10B 6A 6B - - - - EdSocială
22 IP1 - - 12A 9A 12A 11A - InfoAplicații
23 Ge2 - - - - 10E 8A - Geografie
24 Ro8 - - - - 7C 9B - Română
25 Te1 6B 5A 6A - - - - Tehnologie
26 GF2 6D 5D - - - - - ******- Ger/Fra (Germană)
27 GF2GF3 - - - - - 10E - Ger/Fra
28 Bi3 9A 10B 8A - - - - Biologie
29 Bi2 5C 7B 10A - - - - Biologie
30 Sp3 - - - 6C 8C 7A - Spaniolă
31 ES2 10D 7C - - - - - EdSocială
32 Ro4 - - - 7B 6D 9E - Română
33 Ch3 - - - 11B 12B 8B - -*-***- Chimie
34 Sp2 - - 11C 5C 5B 7B - Spaniolă
35 Is2 9E 11E 7B 5B - - - Istorie
36 Ch2 12C 10A 8C - - - - Chimie
37 Ge1 11D 6B 10C - - - - Geografie
38 TI1 - - - 9B 9E 10D - TIC
39 Lo1 - - 9E 12E 11A 12A - Logică
40 En5 5B 11D 12C 5D - - - Engleză
41 En4 - - 9A 8B 6C 12E - Engleză
42 Ma2 - - 6C 9C 6A 10B - Matematică
43 GF2GF4 - - 12E - 11E - - Ger/Fra
44 GF1GF3 - - - 10A 9C - - Ger/Fra
45 Ro7 - - - 12C 8B 11E - Română
46 Re1 - 6C 11D - 5A 9A - Religie
47 Is1 12E 11A 8B 8A - - - Istorie
48 Ro5 - - - 10D 6B 6C - Română
49 Ro6 11C 9A 5B 5A - - - Română
50 GF1 - - 7C - - 5C - -*****- Ger/Fra (Germană)
51 Ro3 - 12E 12B 6A 12E 9C - Română
52 Ma3 - - 9B 6D 11D 9D - Matematică
53 Ma5 - - 5A 6B 12D 10C - Matematică
54 Ma4 8A 11B 5C 12B - - - Matematică
55 Ma1 10A 5B 7A 11A 9A - - Matematică
56 Ma7 - - - 7C 11C 12C - Matematică
57 Ma6 - - - 12A 5D 8C 8B Matematică
58 En3 7B 12B 10E 11E - - - Engleză
59 Ch1 9B 11C 9D 10E - - - Chimie
60 En2 - - 6D 9D 10D 11B 8C Engleză
61 Fi3 - - - 12D 10A 11C 10E Fizică
62 Fi1 11A 12C 9C - 10B - - Fizică
63 En1 - - 11A 9E 9B 12D - Engleză
64 Sp1 6C 10E 11E 11D - - - Spaniolă
65 Ro1 9D 5C 5D 8C 10C - - Română
66 Ro2 12D 7A - 10B 11B 10A - Română
67 Bi1 9C - 10D 11C 9D 6D - ******- Biologie
68 Mu1 7A 8B - - 5C 5A - ***-**- Muzică
Să observăm de exemplu, că Mu1 are nu două ferestre, cum vedem pe linia 68, ci are doar una – cum arată șablonul care îi este asociat în coloana SB; ora a 3-a o face împreună cu De1 (v. linia 4); iar De1 are nu două ore cum vedem pe linia 12, ci trei (conform șablonului existent pentru el în coloana SB). Se vede că apar 4 ferestre la profesori angajați în cuplaje și încă 3 ferestre la ceilalți (pe liniile 46, 62 și 66), toate 7 fiind de câte o singură oră.
Cam la fel stau lucrurile și pe celelalte zile…
reduce_gaps.R angajează și anumite elemente aleatorii (de exemplu, mutări de clasă la întâmplare), încât repetând execuția obținem orare cu altă dispoziție a orelor (și pe unele zile, chiar cu mai puține ferestre decât cele de pe care am redat mai sus o mostră).
vezi Cărţile mele (de programare)