Reluăm "slightchess", chiar de la capăt; anterior (v. all_titles, 2014 / iulie - septembrie) analizam fişierul PGN angajând modulul Python pyparsing şi formulam câteva programe Python pentru a extrage partidele respective în tabele MySQL, constituind aplicaţia Web menţionată folosind Django 1.8. Acum vom folosi R (obţinând din fişierul PGN dat un obiect 'data.frame', uşor de exploatat), PostgreSQL şi Django 2.0.

Am încorporat aici desfăşurarea cronologică a lucrurilor (săptămânal şi cu retuşări) şi am încercat să le prezentăm cu toate motivaţiile şi conexiunile necesare, bazându-ne de obicei pe experimente iterative şi investigaţii proprii (am început în 20 octombrie, cu §1 şi §2; în 26 noiembrie am adăugat §10; în 27 decembrie am adăugat secţiunea finală §18, iar în ianuarie 2018 am şi definitivat slightchess).

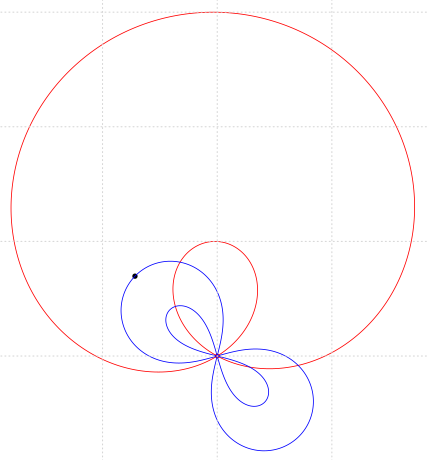
Pentru f(z)=z³ + pz + q, z∈C, (p,q∈C) cu două rădăcini de modul 1, una fixată şi una mobilă: locul valorilor p este o trisectoare Pascal, iar locul punctelor critice este reuniunea a două lemniscate Booth (altfel spus: radicalul unei trisectoare Pascal cu vârful în origine este format din două lemniscate Booth cu aceeaşi axă şi acelaşi centru).

Radicalul unui cerc este un oval Cassini şi poate fi construit (punct cu punct) interpretând puterea punctului faţă de cerc; radicalul unui cerc care trece prin origine este o lemniscată Bernoulli.

Încercăm să clasificăm - sau eventual, să caracterizăm direct - curba descrisă de punctele critice ale unui polinom redus de gradul trei care are o rădăcină fixată şi una mobilă, ambele de modul 1.