Legăturile ecuaţiei cubice (partea a II-a)
Extinzând la numere complexe formula trigonometrică a rădăcinilor dată de Viète, ajungem să evidenţiem teorema lui Marden: punctele critice ale unui polinom de gradul trei cu rădăcini complexe necoliniare, sunt focarele elipsei lui Steiner înscrise triunghiului format de rădăcini (unica elipsă centrată în baricentru şi tangentă laturilor în mijloacele acestora).
Legăturile ecuaţiei cubice (partea I)
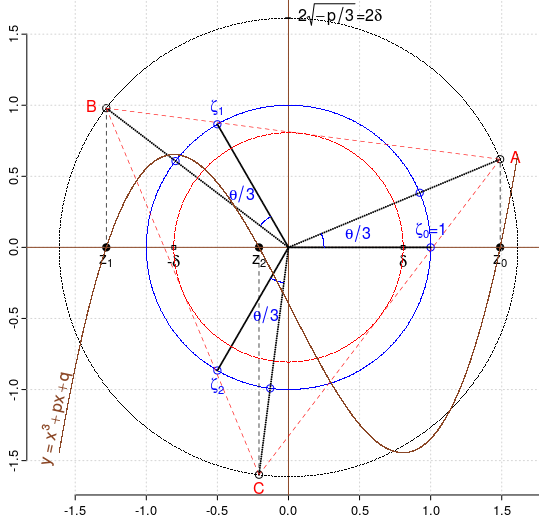
roteşte ζk (rădăcinile de ordinul 3 ale unităţii) cu unghiul θ/3;
proiectează (din origine) imaginile rezultate, pe cercul de rază 2δ (unde ±δ sunt rădăcinile derivatei), obţinând punctele A, B, C;
abscisele punctelor A, B, C sunt rădăcinile reale zk ale ecuaţiei x3+px+q=0, cu p<0, |0.5q / δ3| < 1 şi
θ = arccos( 1.5q / (pδ) ).
Triunghiul ABC este echilateral; cercul înscris lui conţine punctele critice (±δ, 0).
(dar numai întâmplător, ζk par a fi situate pe laturile triunghiului ABC)
Fractalii Newton ai rădăcinilor unităţii - partea a patra
Tranşăm practic (verificând un rezultat teoretic clasic), dilema locului punctelor periodice: generăm fractalul plecând de la unul dintre punctele 2-periodice - colectând preimaginile acestuia până la un anumit ordin de iterare; adăugând pe imaginea obţinută punctele 2-periodice, vedem că acestea ţin de "mulţimea Julia".
Fractalii Newton ai rădăcinilor unităţii - partea a treia
outer(p1, p2) produce matricea m2 în care liniile sunt asociate coeficienţilor p1, iar coloanele - coeficienţilor p2; valorile acestei matrici sunt produsele coeficienţilor respectivi, m2[i][j] = p1[i]*p2[j]. Adunând valorile m2[i][j] pentru i + j = d =constant, obţinem coeficientul monomului de gradul d din produsul celor două polinoame - operaţie montată prin tapply(): clasează valorile după suma indicilor de linie şi coloană şi apoi aplică sum() pe fiecare categorie de valori.
Trasăm numeric coeficienţii ecuaţiei N(N(z)) = z şi folosind apoi polyroot(), găsim punctele 2-periodice ale transformării lui Newton.
Fractalii Newton ai rădăcinilor unităţii - partea a doua
Imaginile rezultate "trunchiază" mulţimea denumită de obicei mulţimea Julia a transformării respective; aceasta este frontiera comună a bazinelor de atracţie ale rădăcinilor polinomului, pe întregul plan (în vecinătatea oricât de mică a oricărui punct al ei există "pre-imagini" ale fiecărei rădăcini - cu interpretarea şocantă că în fiecare punct "se întâlnesc" câte n culori; "pre-imagine" a rădăcinii însemnând aici un punct a cărui orbită converge la o rădăcină a polinomului).
vezi Cărţile mele (de programare)