Punctele cercului unitate au exprimarea parametrică $z=\cos\theta+i\sin\theta=e^{i\theta},\,\theta\in(-\pi,\pi]$ (v. figura (a)). Punctul $z+1$ rezultă translatând $z$ orizontal spre dreapta, cu o unitate; din rombul format (v. (b)) avem coordonatele polare ale lui $z+1$: unghiul polar este $\frac{\theta}{2}$ şi raza polară este $\rho=2\cos\frac{\theta}{2}$. Rotind punctul $z+1$ în jurul originii cu unghiul $\theta$ (v. figura (c)), obţinem imaginea produsului $z(z+1)$ - cu unghiul polar $\frac{\theta}{2}+\theta$ şi cu raza polară egală cu $\rho$.

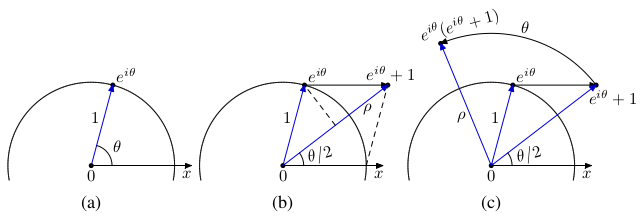
Aşadar, punctele $z(z+1)$ cu $|z|=1$ se reprezintă parametric prin $$p(\theta)=e^{2i\theta}+e^{i\theta}={2\cos\frac{\theta}{2}\left(\cos\frac{3\theta}{2}+i\sin\frac{3\theta}{2}\right)},\,\theta\in(-\pi,\pi]$$

În [1] am stabilit deja că locul punctelor $p(\theta)$ este o trisectoare Pascal; iar în [2] am stabilit (în legătură cu locul punctelor critice ale unei anumite clase de funcţii cubice) că locul punctelor $\sqrt{p(\theta)+1\,}$ este format din două lemniscate Booth coaxiale. Eliminăm acum "$\small +1$" de sub radical, vizând locul punctelor $\sqrt{p(\theta)\,}$; vom vedea însă că această simplificare complică recunoaşterea curbei.

Pe $(-\pi,\pi]$ avem $\cos\frac{\theta}{2}\ge 0$; rezultă că $\sqrt{z(z+1)}$ cu $|z|=1$ se reprezintă prin $$q(\theta)=\sqrt{p(\theta)}=\pm{\sqrt{2\cos\frac{\theta}{2}}\left(\cos\frac{3\theta}{4}+i\sin\frac{3\theta}{4}\right)},\,\theta\in(-\pi,\pi]$$

Cele două ramuri ale lui $q(\theta)$ sunt simetrice faţă de origine, încât ar fi suficient să o vizăm pe aceea cu "$+$"; încercăm întâi, să "ghicim" categoria de curbă corespunzătoare.

În realitate, am desfăşurat acum obişnuitele calcule ingenioase (mai mult sau mai puţin tipice), pentru a elimina parametrul $\theta$; dar ecuaţia carteziană obţinută (după cum vom arăta mai încolo) este "ireductibilă" şi nu am reuşit să o încadrez în vreo clasă cunoscută (spre deosebire de [2], unde prezenţa şi a termenului "$\small+1$" sub radical atrăgea descompunerea ecuaţiei într-un produs pe care am putut recunoaşte ecuaţii de "lemniscate Booth", confirmând apoi şi grafic).

Următorul program R produce graficele pentru $p(\theta)$ şi $q(\theta)$; se configurează o "fereastră grafică" (pentru $x$ şi $y$ între $\small -2$ şi $\small 2$) şi se stabileşte un număr de valori pentru parametrul $\small\theta$ (aici, distanţate cam la jumătatea unei zecimi de miime - ceea ce desigur, pare cam exagerat); apoi, se determină vectorii de coordonate corespunzătoare valorilor parametrului şi se plotează punctele asociate acestora:

plot(0, type="n", xlim=c(-2, 2), ylim=c(-2, 2), asp=1, xlab="", ylab="",
     cex.axis=0.8, bty="n"); grid()  # setează fereastra grafică
n <- 6283*2  # lungimea cercului unitar este aproximativ 6.283
theta <- seq(-pi, pi, length=n)
zp <- 2*cos(theta/2)*exp(1i*3*theta/2)  # coordonatele lui p(θ)
points(zp, type="l", col="firebrick2", lwd=1.2)  # trisectoare Pascal ("limaçon")
zq <- sqrt(2*cos(theta/2))*exp(1i*3*theta/4)  # coordonatele lui q(θ)
points(zq, col="gray1", type="l", lwd=1.3)  # ramura "principală" q(θ)
points(-zq, col="gray60", type="l")  # opusa ramurii principale

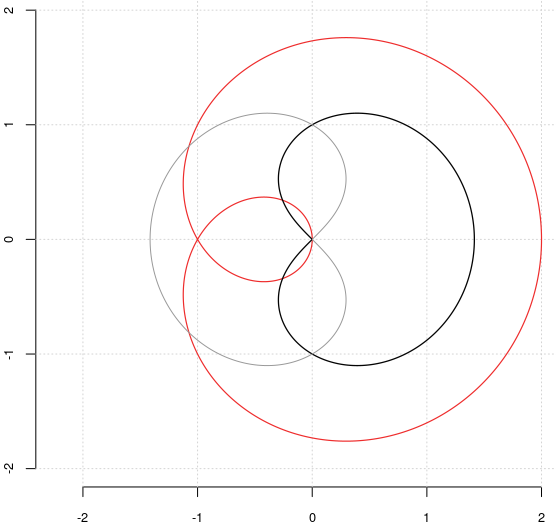
Am colorat cu o nuanţă de roşu curba descrisă de $p(\theta)$ (o "trisectoare Pascal", cum am evocat mai sus). Cu negru am marcat "ramura principală" a lui $q(\theta)$; aceasta seamănă cu o cardioidă…

Dar ştim că într-o cardioidă coardele care trec prin "punctul de întoarcere" au aceeaşi lungime;
aici însă, coarda verticală dusă prin origine are lungimea 2  – fiindcă $\small q(\theta)$ trece prin punctele $\small\pm i$: $\small q(2\pi/3)=\sqrt{p(2\pi/3)}=\sqrt{-1}=\pm i$ –   iar cea orizontală prin origine are lungimea $\small|q(0)|=\sqrt{2}$. Aşa că, ramura lui $q(\theta)$ nu este o cardioidă.

Dintre categoriile de curbe existente (a vedea cataloage precum 2dcurves), "cardioida" ar fi totuşi, cea mai potrivită pentru a încadra cumva curba obţinută aici (dar ar fi un "subtip" de cardioidă); încercăm să investigăm direct, proprietăţile acestei pseudo-cardioide.

Să găsim întâi, ecuaţiile carteziene pentru $q(\theta)=x(\theta)+iy(\theta)$. Putem elimina parametrul $\small\theta$ de exemplu astfel: din $\small x^2+y^2=2\cos\frac{\theta}{2}=2(2\cos^2\frac{\theta}{4}-1)$ şi $\small\cos 3\frac{\theta}{4}=\cos\frac{\theta}{4}\left(4\cos^2\frac{\theta}{4}-3\right)$ rezultă că $\small x^2=2\cos\frac{\theta}{2}\,\cos^2\frac{3\theta}{4}=(x^2+y^2)\frac{1}{4}(x^2+y^2+2)(x^2+y^2-1)^2$; în final avem $$q(\theta):\hskip1em(x^2+y^2)^4-3(x^2+y^2)^2-2(x^2-y^2)=0$$

Mai sus am plotat separat cele două ramuri ale radicalului, evidenţiind "sub-cardioida"; acum, obţinând ecuaţia implicită - putem plota curba ca secţiune plană a unei anumite suprafeţe (deci, fără a mai distinge între ramuri). Procedând şi aşa, putem sesiza eventual apropierea de vreo altă categorie de curbe (poate mai potrivită, decât pseudo-cardioida inventată mai sus).

Creem o funcţie plot_path() care să ploteze funcţia implicită f(x,y) primită ca parametru: se constituie o reţea de puncte (x,y), se calculează şi se tabelează valorile funcţiei în punctele reţelei (folosind outer()) şi apoi se plotează (prin contour()) punctele reţelei în care valorile sunt nule (se obţine curba "de nivel 0" a suprafeţei Z=f(x,y), deci graficul ecuaţiei f(x,y) = 0).

plot_path <- function(func2, asp=1, ...) {  # plotează funcţii implicite
    x <- y <- seq(-1.5, 1.5, by=0.01)  # o reţea de 300×300 puncte (x,y)
    Z <- outer(x, y, func2)  # valorile f(x,y), indexate după x şi y
    contour(x, y, Z, ...)  # cu 'levels=H' vom avea graficul f(x,y) = H
}  ## '...' transmite argumente specifice funcţiei contour() (precum "levels")

plot_path(function(u, v) (u^2+v^2)^4 - 3*(u^2+v^2)^2 - 2*(u^2-v^2),  # q(θ)
          levels=c(0), col=c("black"), lwd=0.5, drawlabels=FALSE)

plot_path(function(u, v) (u^2+v^2)^3 -2*(u^2+v^2)^2 + v^2,  # Dürer's folium
          levels=c(0), col=c("blue"), lwd=0.5, drawlabels=FALSE, add=TRUE) 

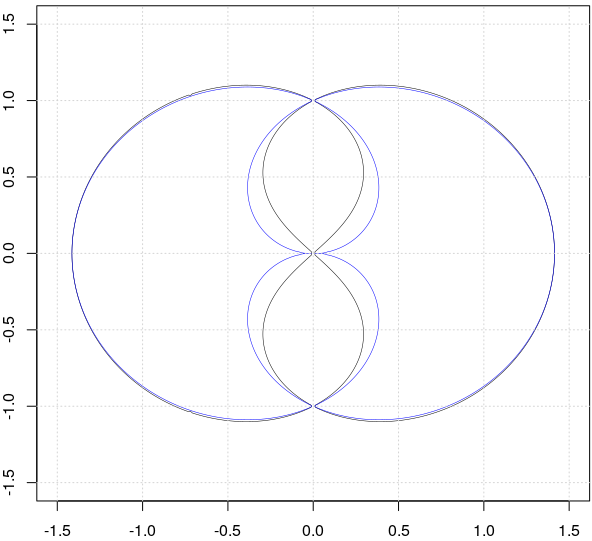
Cu negru am plotat $q(\theta)$ (dar la altă scară faţă de imaginea anterioară), iar cu albastru o curbă din categoria "Dürer folium". Contururile aproape că se suprapun pe porţiunea exterioară, dar pe "buclele" interioare diferenţele sunt evidente; tendinţa diferenţelor ar putea fi evidenţiată plotând mai multe curbe de nivel (folosind de exemplu levels = seq(-.5, .5, by=.05), în cele două apeluri plot_path()).

Să observăm că ecuaţia carteziană obţinută mai sus pentru $q(\theta)$ "acoperă" ambele ramuri (dat fiind că $x$ şi $y$ apar numai la puteri pare, în toate monoamele dezvoltării). Aici vom încerca să vizăm numai ramura din dreapta, ca şi când ar fi o curbă independentă (o "sub-cardioidă"); dar aceasta îşi va merita "independenţa" şi numele, numai dacă vom putea-o caracteriza printr-o anumită proprietate geometrică specifică ei.

Probabil că va fi dificil de caracterizat geometric $q(\theta)$ (prin vreo proprietate similară uneia dintre cele care definesc cardioida: "curba descrisă de un punct fixat pe un cerc care se rostogoleşte pe un cerc fix de aceeaşi rază"); ne limităm deocamdată la evidenţierea tipică a anumitor puncte şi tangente.
Arătăm că "sub-cardioida" (referită mai jos prin $\mathcal{Q}$) are ca (semi)tangente în origine bisectoarele sistemului de axe; apoi îi vom determina "punctele extreme":

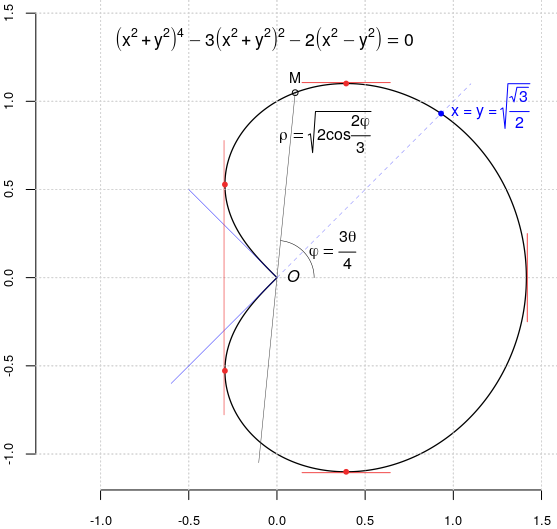
Când M tinde pe $\small\mathcal{Q}$ către O, secanta MO tinde spre una sau alta dintre cele două semitangente în O; raza polară $\rho=\sqrt{2\cos\frac{2\varphi}{3}}$ (unde am notat $\varphi=\frac{3\theta}{4}$) ajungând zero, vom avea $\frac{2\varphi}{3}=\frac{\pi}{2}$; rezultă că $\varphi=\pm\frac{3\pi}{4}$, deci semitangentele în origine sunt respectiv pe bisectoarele sistemului de axe. Să determinăm cealaltă intersecţie cu $\small\mathcal{Q}$ a primei bisectoare (analog pentru a doua): pentru $\varphi=\frac{\pi}{4}$ avem $\theta=\frac{\pi}{3}$, deci intersecţia respectivă este $q(\frac{\pi}{3})=\sqrt{2\cos{\frac{\pi}{6}}}e^{i\frac{\pi}{4}}$, adică este punctul de coordonate $x=y=\sqrt{\frac{\sqrt{3}}{2}}$.

Obs. Era suficient să ne uităm la partea de grad minim a ecuaţiei, $-2(x^2-y^2)$, pentru a spune imediat că tangentele în origine sunt $y=\pm x$. Într-adevăr: punând $y=mx$ (reprezentând o dreaptă care trece prin origine) obţinem $x^8(1+m^2)^4-3x^4(1+m^2)^2-2x^2(1-m^2)=0$; simplificând prin $x^2$ şi făcând apoi $x=0$ rămâne $-2(1-m^2)=0$, adică $y=\pm x$ (bisectoarele sistemului de axe).

Să determinăm punctele în care tangenta este paralelă uneia dintre axe (necesare între altele, când am vrea să creem un simbol pentru curba respectivă, ca în [3]). Derivăm în raport cu $x$ ecuaţia $q(\theta)$ (considerând $y$ ca funcţie de $x$, deci de exemplu $(y^2)'=2yy\,'$) şi separăm: $$y\,'=\frac{x(1-2(x^2+y^2)^3+3(x^2+y^2))}{y(1+2(x^2+y^2)^3-3(x^2+y^2))}$$

Fie $t=x^2+y^2\ne 0$. Pentru $y=0$ avem $y\,'=\infty$; deci în punctul $(\sqrt{2\,},0)$ avem tangentă verticală. Avem tangente paralele uneia dintre axe în acele puncte ale curbei pentru care $2t^3-3t\pm 1=(t\pm 1)(2t^2\mp 2t-1)=0$. După un calcul care nu necesită decât atenţie, rezultă că pe verticală, punctele extreme ale curbei (în care avem tangentă orizontală) sunt $\left(\frac{\sqrt{2\sqrt{3}-1}}{4},\,\pm\frac{\sqrt{6\sqrt{3}+9}}{4}\right)$; iar dreapta dusă prin punctele $\left(-\frac{\sqrt{6\sqrt{3}-9}}{4},\,\pm\frac{\sqrt{2\sqrt{3}+1}}{4}\right)$ este tangentă verticală la $\mathcal{Q}$ (punctele respective sunt cele marcate cu roşu pe figura de mai sus).

În absenţa unor cunoştinţe mai serioase (de "geometrie diferenţială"), nu vedem cum să speculăm mai departe ecuaţiile obţinute; dar probabil că şansele unei caracterizări geometrice ale pseudo-cardioidei rezultate mai sus sunt ascunse chiar în figura elementară (c) de la care am plecat…