Pe trisectoare - cu rigla, compasul şi MetaPost
[1] O chestiune de loc geometric (transformarea cercului în trisectoare)
[2] Metafont pentru trisectoarea lui Pascal
[3] O pseudo-cardioidă
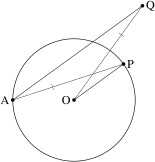 Fixăm $\sf O$ şi $\sf A$; pentru fiecare punct $\sf P$ al cercului care trece prin $\sf A$ şi are centrul în $\sf O$ construim punctul $\sf Q$ astfel încât $\sf AQ \parallel OP$ şi $\sf AP=OQ$.
Fixăm $\sf O$ şi $\sf A$; pentru fiecare punct $\sf P$ al cercului care trece prin $\sf A$ şi are centrul în $\sf O$ construim punctul $\sf Q$ astfel încât $\sf AQ \parallel OP$ şi $\sf AP=OQ$.
Avem de caracterizat mulţimea punctelor $\sf Q$ astfel definite.
Vom vedea (amintindu-ne de riglă şi compas) că rezultă două puncte $\sf Q$ - surpriza fiind aceea că în timp ce unul descrie un cerc (banal), celălalt descrie o trisectoare Pascal ($\mathcal{T}$); plecând de la trapezul isoscel format, constatăm în mod elementar proprietăţi caracteristice ale acesteia.
Construcţii
Dacă am cere cuiva să figureze enunţul cu mâna liberă, cel mai probabil rezultat ar fi o figură asemănătoare celeia redate mai sus.
 Dar să "construim punctul $\sf Q$", cum îndeamnă enunţul. Fixăm vârful în $\sf O$, deschidem compasul cu raza $\sf OA$ şi trasăm cercul; folosind rigla, marcăm diametrul $\sf AA'$.
Dar să "construim punctul $\sf Q$", cum îndeamnă enunţul. Fixăm vârful în $\sf O$, deschidem compasul cu raza $\sf OA$ şi trasăm cercul; folosind rigla, marcăm diametrul $\sf AA'$.
Cu vârful compasului în $\sf A'$ şi cu o deschidere mai mică decât diametrul, marcăm pe semicercul superior un punct $\sf P$; notăm cu $\theta\in(0,\pi)$ lungimea arcului subîntins.
Fără să modificăm deschiderea, dar acum cu vârful compasului în $\sf P$, marcăm pe cerc punctul $\sf P'$.
Fiindcă $P$ este mijlocul arcului $\small\overparen{\sf A'P'}$ iar $\sf O$ este mijlocul diametrului $\sf AA'$, rezultă că $\sf AP'\parallel OP$; luând în compas segmentul $\sf AP$ şi rotindu-l cu vârful în $\sf O$ - obţinem două puncte $\sf Q$ şi $\sf Q'$ pe dreapta $\sf AP'$ (satisfăcând fiecare, proprietatea indicată în enunţ pentru "punctul $\sf Q$").
Desigur, figurile redate aici au fost construite nu atât cu rigla şi compasul, cât folosind un limbaj de programare grafică; este uşor astfel să şi schiţăm locurile respective. Preferăm MetaPost (v. şi [2], [3]), în care putem genera puncte şi linii prin proprietăţi geometrice (şi nu neapărat, prin ecuaţia curbei) şi în care avem asigurate deasemenea, diversele transformări geometrice.
Figurile sunt constituite într-un fişier "locus.mp", fiecare fiind ambalată între beginfig(<număr>) şi endfig; fişierele grafice corespunzătoare lor (într-un format sau altul) vor fi obţinute invocând compilatorul de MetaPost (prin 'mpost -tex=latex locus'). Preferăm aici formatul de imagine PNG (un fişier SVG - cu avantaje de redare legate de rezoluţie - este totuşi prea voluminos):
%% locus.mp outputformat := "png"; % pentru figuri în formatul de imagine PNG outputtemplate := "%j-%c.png"; % va rezulta "locus-1.png", "locus-2.png", etc. outputformatoptions := "format=rgba antialias=good"; % asigură "background=transparent" verbatimtex % pentru fişiere temporare de transferat compilatorului de LaTeX \documentclass[11pt]{article} \begin{document} etex
Preferăm să folosim un "font matematic" pentru a eticheta puncte, linii, etc.; anturajul verbatimtex asigură transferarea unui text către LaTeX: mpost va crea un fişier LaTeX temporar conţinând sub \begin{document} expresiile respective, va invoca pe acest fişier compilatorul de LaTeX şi va folosi rezultatul pentru a monta în 'currentpicture' etichetele corespunzătoare.
De exemplu, să ataşăm eticheta "$\small\mathsf{A}$" în stânga punctului de coordonate (în centimetri) (-2, 0):
pair A; A=(-2cm, 0); dotlabel.lft(btex $\mathsf{A}$ etex, A);
Folosind instrucţiunile din verbatimtex, mpost va crea un document LaTeX (temporar) conţinând secvenţele cuprinse între btex ("begin TeX") şi etex ("end TeX") şi-l va pasa compilatorului de LaTeX (cum fusese precizat prin opţiunea de compilare "-tex=latex"); mpost va folosi rezultatul returnat de către LaTeX (în cazul de faţă: glyph-ul pentru "A" din fontul matematic curent, în varianta "sans serif") pentru a constitui o structură de date de tip "picture" pe care o va insera ulterior în structura "currentpicture" asociată figurii.
Nu avem o metodă de automatizare a etichetării; avem de folosit atâtea secvenţe dotlabel() sau label(), câte etichete avem de pus pe figură. Aici vom exclude instrucţiunile de etichetare, din secvenţele de cod pe care le vom reda.
În figura următoare schiţăm locul lui $\sf Q$ - bazându-ne pe definiţia de mai sus (din care se deduce uşor că $\sf OPQP'$ este un romb); macro-ul Q(theta) "traduce" în MetaPost construcţia respectivă şi este folosit (într-o instrucţiune for) pentru a plota punctele $\sf Q$ rezultate rotind $\sf P$ pe cercul de centru $\sf O$ şi rază $\sf OA$ cu câte 5 grade (mai precizăm că dir$\,\theta$ dă punctul $(\cos\theta,\,\sin\theta)$, iar fullcircle este un contur predefinit care aproximează cercul cu diametrul 1/72 inch centrat în origine):
beginfig(2); ao = 1.8cm; % alege distanţa AO; avem A(-ao, 0) şi A'(ao, 0) draw fullcircle scaled 2ao withpen pencircle scaled 0.2 withcolor .7white; %% ... plotează alte puncte, drepte, etichete, etc. vardef Q(expr theta) = % returnează punctul Q (=P+P'), din rombul OP'QP pair P, P'; P = ao*dir(theta); % P este pe cercul de centru O, rază AO P' = (ao, 0) reflectedabout(origin, P); % simetricul lui A' faţă de OP P + P' enddef; for fi=0 step 5 until 360: % plotează punctele Q, rotind P cu câte 5 grade draw Q(fi) withpen pencircle scaled 1.4 withcolor .6blue; endfor; currentpicture := currentpicture scaled 1.2; % măreşte puţin, întreaga figură endfig; %% ... o altă figură end %% salvează "locus.mp" şi compilează: mpost -tex=latex locus (rezultă "locus-2.png")

Avem de constatat şi de justificat un fapt surprinzător: în timp ce unul dintre capetele segmentului $\sf QQ'$ descrie (oarecum banal) un cerc, capătul celălalt descrie o trisectoare Pascal (şi vom proba prin raţionamente geometrice elementare unele caracteristici ale acesteia).
$\mathcal{T}$ este o sectrice
Având două laturi paralele şi diagonalele egale, $\sf AOPQ$ este trapez isoscel; rezultă că $\sf OPQP'$ este romb. Din triunghiurile isoscele formate şi ţinând cont că $\sf AP$ bisectează unghiul $\sf \widehat{A'OP'}$, rezultă că $\sf\widehat{QOA'}=\frac{3\theta}{2}$ (iar $\sf\widehat{QAA'}=\theta$).
Prin urmare, $\sf Q$ poate fi văzut ca fiind intersecţia a două drepte care se învârt în jurul a câte unui punct fix astfel încât raportul vitezelor de rotaţie este fie $\sf 3/2$, fie $\sf 2/3$. Pentru poziţia iniţială $\sf \theta=0$ avem $\sf P\equiv A'$, iar $\sf Q\in AA'$ (cu $\sf A'$ între $\sf O$ şi $\sf Q$) şi $\sf OQ=AA'$.
Plecând de la faptul că $\sf OQQ'$ este triunghi isoscel, "vedem" uşor că $\sf Q'O\parallel AP$ şi deci, $\sf Q'APO$ este paralelogram. Rezultă în primul rând, că $\sf Q'A=PO$(=constant), adică locul lui $\sf Q'$ este cercul de centru $\sf A$ şi rază $\sf AO$; în al doilea rând, rezultă că faţă de axa $\sf AA'$ dreptele $\sf QA$ şi $\sf Q'O$ sunt înclinate cu unghiurile $\theta$ şi respectiv $\theta/2$ - adică:
$\sf Q'$ poate fi văzut ca fiind intersecţia a două drepte care se învârt în jurul a câte unui punct fix astfel încât raportul vitezelor de rotaţie este fie $2$, fie $1/2$.
Curbele rezultate din intersecţia a două drepte care se învârt în jurul a câte unui punct fix (având fiecare ca poziţie iniţială, dreapta dusă prin cele două puncte fixe) astfel încât raportul vitezelor de rotaţie este constant $\small\sf k$, sunt cunoscute sub numele (latinesc) sectrices (v. sectrix of Maclaurin). Pentru $\small\sf k=2$ (sau $\small\sf k=1/2$) rezultă un cerc, cum am arătat mai sus pentru punctul $\sf Q'$; iar pentru $\small\sf k=3/2$ (sau $\small\sf k=2/3$) - cum este cazul punctului $\sf Q$ - rezultă o trisectoare Pascal.
Ajungem pe $\mathcal{T}$ rotind şi translatând punctele cercului
Ar fi uşor aici, să constatăm şi direct că locul lui $\sf Q$ este într-adevăr, o trisectoare Pascal: în sistemul de coordonate definit de $\small\sf (\overrightarrow{OA'},\overrightarrow{OB'})$ (cu $\small\sf OB'\perp AA'$ şi $\small\sf OB'=OA=1$), fie $z$ afixul lui $\sf P$; atunci afixul lui $\sf P'$ este $z^2$ (fiindcă unghiul polar al lui $\sf P'$ este dublul celui al lui $\sf P$) şi fiindcă $\small\sf \overrightarrow{P'Q}=\overrightarrow{OP}$, rezultă că afixul lui $\sf Q$ este $z^2+z$ - ori am demonstrat deja în [1], că locul punctelor $z(z+1)$ pentru care $|z|=1$ (deci locul lui $\sf Q$) este o trisectoare Pascal.
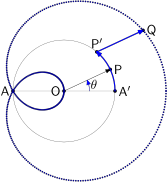 Expresia $z^2+z$ se poate "traduce" geometric astfel: se roteşte punctul $\sf A'$ în jurul lui $\sf O$ cu $2\theta$ (unde $\theta=\arg(z)$), rezultând punctul $\sf P'$ de afix $z^2$; se translatează $\sf P'$ în direcţia $\theta$ cu o lungime egală cu $\sf OA$ - ajungând în punctul $\sf Q$ al trisectoarei. Macro-ul
Expresia $z^2+z$ se poate "traduce" geometric astfel: se roteşte punctul $\sf A'$ în jurul lui $\sf O$ cu $2\theta$ (unde $\theta=\arg(z)$), rezultând punctul $\sf P'$ de afix $z^2$; se translatează $\sf P'$ în direcţia $\theta$ cu o lungime egală cu $\sf OA$ - ajungând în punctul $\sf Q$ al trisectoarei. Macro-ul Q(theta) corespunzător în programul de mai sus ar fi:
vardef Q(expr theta) =
(ao, 0) rotated 2theta shifted(ao*dir(theta))
enddef;
Această construcţie elegantă permite următoarea interpretare: dacă $\sf P_0P_1P_2\dots P_n$ este un poligon regulat înscris într-un cerc de centru $\sf O$, atunci capetele segmentelor de lungime egală cu raza cercului, duse prin fiecare vârf $\sf P_{2j}$ paralel cu $\sf OP_j$, sunt situate pe o trisectoare Pascal (indicele $\sf j$ parcurgând circular, valorile 0..n); desigur, mai bine inversăm: "duse prin $\sf P_j$ paralel cu $\sf OP_{2j}$" (valabil fiindcă $\sf OPQP'$ este romb), obţinând câte un $\sf Q$ pentru toate vârfurile şi nu doar pentru cele de index par.
$\mathcal{T}$ este podara unui cerc
Mai rezultă (revenind la $\sf Q'$) această posibilitate (inedită) de construcţie punctuală a trisectoarei lui Pascal: pe cercul de centru $\sf A$ şi rază $\sf AO$ luăm arbitrar un punct $\sf Q'$; folosind compasul, marcăm pe semidreapta $\sf Q'A$ punctul $\sf Q$ pentru care $\sf OQ=OQ'$; punctele $\sf Q$ asociate prin această construcţie punctelor cercului menţionat formează o trisectoare Pascal.
Faptul că $\sf OQ'=OQ$ ne sugerează încă o construcţie. Să prelungim $\sf Q'O$ cu $\sf OT=Q'O$; astfel, $\sf Q$ se află pe semicercul de diametru $\sf Q'T$ ceea ce înseamnă că $\sf \measuredangle Q'QT=90^{\circ}$:
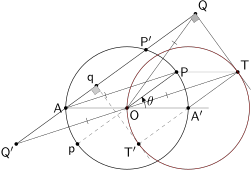
$\sf AOTP$ este paralelogram (fiindcă $\sf AP$ este paralelă şi egală cu $\sf Q'O$, deci şi cu $\sf OT$); deci $\sf PT$ este paralelă şi egală cu $\sf AO$, deci şi cu $\sf OA'$; rezultă că $\sf OPTA'$ este romb. Prin urmare, $\sf T$ se află pe cercul de centru $\sf A'$ şi de rază egală cu $\sf AO$; mai mult, $\sf QT$ este tangentă acestui cerc (fiindcă $\sf TA'\parallel PO\parallel QA$ şi cum am stabilit mai sus, $\sf QA\perp QT$).
Deci $\sf Q$ poate fi văzut ca fiind piciorul perpendicularei din $\sf A$ pe o tangentă a cercului (fix) de centru $\sf A'$ şi rază egală cu $\sf AO$. Regăsim astfel, această proprietate: trisectoarea lui Pascal este podara (sau "pedala") unui cerc faţă de un punct exterior cercului (în general, podara unei curbe este locul geometric al proiecţiilor unui punct dat, pe tangentele acelei curbe).
Dar tangenta în punctul $\sf T'$ diametral opus lui $\sf T$ în cercul de centru $\sf A'$ şi rază $\sf A'O$ este şi ea, perpendiculară pe $\sf AQ$ (fiind paralelă cu $\sf TQ$), în punctul $\sf q$; este uşor de constatat că $\sf OpAq$ este trapez isoscel (unde $\sf p$ este punctul diametral opus lui $\sf P$ pe cercul de centru $\sf O$ şi rază $\sf OA$) - încât $\sf q$ satisface proprietăţile impuse lui $\sf Q$ (având $\sf Aq\parallel Op$ şi $\sf Ap=Oq$).
Prin urmare, pe orice dreaptă dusă prin $\sf A$ găsim două puncte $\sf Q$ şi $\sf q$ ale trisectoarei lui Pascal (definite de $\sf O$ şi $\sf A$) - anume, intersecţiile cu tangentele cercului de centru $\sf A'$ şi rază egală cu $\sf AO$ duse în capetele diametrului paralel dreptei respective; în plus, avem $\sf P'Q=P'q=OP$ - încât regăsim şi această modalitate de construcţie: pe orice secantă prin $\sf A$ la cercul de centru $\sf O$ şi rază $\sf OA$ se marchează cele două puncte aflate la distanţa egală cu $\sf OA$ faţă de intersecţia secantei cu cercul (unul aparţine buclei exterioare, iar celălalt buclei interioare a trisectoarei).
$\mathcal{T}$ este înfăşurătoarea unei anumite familii de cercuri
Punctul $\sf Q$ este situat şi pe cercul de diametru $\sf AT$, care are "avantajul" (faţă de cercul $\sf(Q'QT)$ implicat mai sus) că trece prin punctul fix $\sf A$; ce poziţie are acest cerc, faţă de trisectoare?
Cercul $\sf (ATQ)$ este tangent (în $\sf Q$) trisectoarei.
Dar această proprietate este dificil de evidenţiat "pe figură" (procedând tot aşa de elementar ca şi mai sus); să angajăm în schimb (mai "tehnic"), ecuaţiile cercului şi trisectoarei.
Luăm $\sf OA$ ca unitate de măsură şi considerăm sistemul de axe perpendiculare cu originea $\sf O$, astfel încât punctul $\sf A$ are coordonatele $\sf (-1, 0)$. Cercul $\sf (ATQ)$ are centrul în mijlocul razei $\sf OP$, astfel că el are ecuaţia: $$(x-\frac{1}{2}\cos\theta)^2+(y-\frac{1}{2}\sin\theta)^2=\frac{5}{4}+\cos\theta$$
Derivând în raport cu $x$, găsim panta tangentei într-un punct $(x,y)$ al cercului: $$y\,'=\frac{-2x+\cos\theta}{2y-\sin\theta}$$
$\sf Q$ are coordonatele $x=\cos 2\theta+\cos\theta$ şi $y=\sin 2\theta+\sin\theta$ (fiindcă $\sf \overrightarrow{OQ}=\overrightarrow{OP'}+\overrightarrow{OP}$, iar $\sf P(\cos \theta,\sin\theta)$ şi $\sf P'(\cos 2\theta,\sin 2\theta)$); rezultă că tangenta în $\sf Q$ la cerc are panta: $$y\,'_Q=\frac{-2\cos 2\theta-\cos\theta}{2\sin 2\theta+\sin\theta}\hskip{2em}(1)$$
Coordonatele polare ale lui $\sf Q$ sunt $\rho=2\cos\frac{\theta}{2}$ (aceasta rezultă cel mai simplu din triunghiul isoscel $\sf OPQ$, în care unghiurile de la bază sunt egale cu $\theta/2$) şi $\varphi=\frac{3\theta}{2}$. Rezultă că ecuaţia polară a trisectoarei este $\rho=2\cos\frac{\varphi}{3}$ (cu $\varphi=\frac{3\theta}{2}$ ales astfel încât $\theta\in(-\pi,\pi]$) şi pentru coordonatele carteziene avem $x=2\cos\frac{\varphi}{3}\cos\varphi$, iar $y=2\cos\frac{\varphi}{3}\sin\varphi$.
După regulile de derivare uzuale avem $y\,'=\frac{{\rm{d}}y}{{\rm{d}}x}=\frac{{\rm{d}}y}{{\rm{d}}\varphi}\frac{{\rm{d}}\varphi}{{\rm{d}}x}$ şi $\frac{{\rm{d}}\varphi}{{\rm{d}}x}=\frac{1}{{\rm{d}}x/{\rm{d}}\varphi}$. În cazul nostru, $$\begin{array}{@{}cll} \frac{{\rm{d}}y}{{\rm{d}}\varphi} &=& \frac{{\rm{d}}}{{\rm{d}}\varphi}(2\cos\frac{\varphi}{3}\sin\varphi) \\ &=& -\frac{2}{3}\sin\frac{\varphi}{3}\sin\varphi+2\cos\frac{\varphi}{3}\cos\varphi\\ &=& \frac{2}{3}\left(2\cos\frac{4\varphi}{3}+\cos\frac{2\varphi}{3}\right) \\ &=& \frac{2}{3}(2\cos 2\theta+\cos\theta) \end{array}$$
Analog rezultă $\small\eqalign{\frac{{\rm{d}}x}{{\rm{d}}\varphi}=-\frac{2}{3}(2\sin 2\theta+\sin\theta)}$ şi făcând raportul $\frac{{\rm{d}}y}{{\rm{d}}\varphi}/\frac{{\rm{d}}x}{{\rm{d}}\varphi}$ obţinem aceeaşi valoare ca şi în $\small(1)$ pentru $y\,'_Q$. Cu alte cuvinte, cercul $\sf (ATQ)$ şi trisectoarea au o aceeaşi tangentă în punctul comun $\sf Q$. Ţinând cont de faptul că mijlocul razei $\sf OP$ (care este centrul cercului $\sf(ATQ)$) este distanţat de origine cu $\sf\small AO/2$, putem reformula astfel: cercurile care trec prin $\sf A$ şi au centrul pe cercul de centru $\sf O$ şi rază $\sf \frac{1}{2}AO$ sunt tangente trisectoarei (se mai zice că trisectoarea lui Pascal înfăşoară aceste cercuri, sau că este înfăşurata acestora).
 Deducem şi o construcţie directă a tangentei şi normalei într-un punct al trisectoarei. Fie $\sf Q$ pe bucla exterioară a lui $\mathcal{T}$; ducem paralela prin $\sf O$ la $\sf AQ$ şi luăm pe aceasta punctul $\sf P$ pentru care $\sf OP=OA$; dacă $\sf R$ este mijlocul segmentului $\sf OP$ (tocmai centrul cercului $\sf (ATQ)$, tangent în $\sf Q$ trisectoarei cum am arătat mai sus), atunci $\sf QR$ este normală trisectoarei (perpendiculara pe tangenta acesteia în $\sf Q$).
Deducem şi o construcţie directă a tangentei şi normalei într-un punct al trisectoarei. Fie $\sf Q$ pe bucla exterioară a lui $\mathcal{T}$; ducem paralela prin $\sf O$ la $\sf AQ$ şi luăm pe aceasta punctul $\sf P$ pentru care $\sf OP=OA$; dacă $\sf R$ este mijlocul segmentului $\sf OP$ (tocmai centrul cercului $\sf (ATQ)$, tangent în $\sf Q$ trisectoarei cum am arătat mai sus), atunci $\sf QR$ este normală trisectoarei (perpendiculara pe tangenta acesteia în $\sf Q$).
Dacă $\sf AQ$ intersectează bucla interioară în $\sf Q'$, atunci simetrizăm $\sf P$ şi $\sf R$ faţă de $\sf O$ şi găsim analog, normala în $\sf Q'$ a trisectoarei.
Menţionăm o întrebare imediată: cât este unghiul tangentelor la trisectoare în punctele $\sf Q$ şi $\sf Q'$ (în funcţie de $\theta\,$)?
Reliefarea înfăşurării
Să facem şi o figură vizând construcţia trisectoarei prin înfăşurarea cercurilor de centru $\sf R$ şi rază $\sf RA$. Instituim macro-ul drawenv(S), pentru a furniza cercurile cu centrele situate din S° în S° pe cercul centrat în origine de rază $\sf\frac{1}{2}AO$; folosim image() (creează o variabilă de tip 'picture', al cărei conţinut va putea fi inserat ulterior într-un loc sau altul al figurii), pentru a instanţia într-o aceeaşi figură mai multe înfăşurări particulare ale lui $\mathcal{T}$ (aici, una pentru S=12° şi una pentru S=5°):
beginfig(8); % "locus-8.png" numeric ao; ao = 1.5cm; % redefineşte distanţa AO pair A; A = ao*left; % 'left' este (-1,0) def drawenv(expr S) = label.rt(btex $\mathsf{A}$ etex, A); dotlabel.lft(btex $\mathsf{O}$ etex, origin); for fi=0 step S until 360: pair R; R = .5ao*dir(fi); % mijlocul razei polare curente numeric r; r = abs(R-A); % raza cercului prin A, de centru R draw fullcircle scaled 2r shifted(R) withpen pencircle scaled 0.3; endfor; draw fullcircle scaled ao withpen pencircle scaled 0.7 withcolor red; enddef; picture envel[]; % "tablou" de variabile de tip 'picture' envel1 = image( drawenv(12); % cercurile centrate pe cercul roşu din 12° în 12° z1 = .5ao*dir(36); drawdot(z1) withpen pencircle scaled 2.7 withcolor blue; w = abs(z1-A); % cercul prin A, de centru z1 (cel albastru): draw fullcircle scaled 2w shifted(z1) withpen pencircle scaled 0.7 withcolor blue; label(btex $\mathcal{T}$ \^{i}nf\u{a}\c{s}oar\u{a} 30 de cercuri etex, (.3ao, -2ao)); ); envel2 = image( drawenv(5); % cercurile centrate pe cercul roşu din 5° în 5° label(btex $\mathcal{T}$ \^{i}nf\u{a}\c{s}oar\u{a} 72 de cercuri etex, (.3ao, -2ao)); ); numeric width; width = xpart(urcorner(envel1) - ulcorner(envel1)); draw envel1; draw envel2 shifted((1.2width, 0)); currentpicture := currentpicture scaled 1.2; endfig;
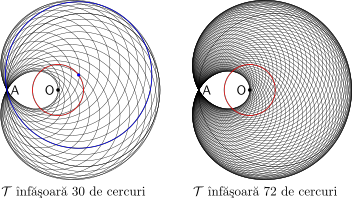
Rotind raza polară $\sf OP$ cu câte 12°, au fost trasate 30 de cercuri având centrul pe cercul marcat cu roşu (cu centrul în $\sf O$, de rază $\sf \frac{1}{2}AO$) şi trecând toate prin $\sf A$ (pentru poza din dreapta am rotit cu câte 5°; trisectoarea apare mai bine conturată, dar mărind numărul de cercuri lizibilitatea acestora scade). Pe figura din stânga este marcat cu albastru un cerc particular - cel cu centrul aflat la 36° pe cercul roşu. Pe ambele figuri se distinge cercul care este tangent trisectoarei în vârful acesteia (cu centrul aflat la 0° pe cercul roşu); el apare mai bine conturat decât celelelte fiindcă provine cel mai natural, din conturul 'fullcircle' (prin scalare şi deplasare orizontală, încât erorile de poziţionare a pixelilor sunt atenuate faţă de cazul celorlalte cercuri).
vezi Cărţile mele (de programare)